Why do we really need more than one attention head?

Understanding Multi-Head Attention: The Heart of Transformers

and

Oct 28, 2025

When we first look at the transformer architecture, it can feel like an intimidating maze of layers, vectors, and strange mathematical symbols. But if we pause for a moment and start from the basics, we begin to see how beautifully simple and intuitive it really is. The real power of a transformer comes from its ability to focus on different parts of the input simultaneously. And that is exactly what multi-head attention does.

In this article, we will walk through the complete intuition, mathematics, and practical implementation of multi-head attention. This is the same concept that lies at the core of large language models like GPT-3 and GPT-4, and vision models like ViT. By the end, you will realize that multi-head attention is nothing more than several simple attention mechanisms working together in parallel.

From Attention to Self-Attention

Before multi-head attention, we must understand what attention itself does. In the simplest sense, attention allows a model to decide how much each input token should influence another token. When we say the model is attending to something, we mean it is computing a score for how relevant one word is to another.

Mathematically, we take the dot product between a query and a key, scale it by the square root of the key dimension, and apply a softmax to normalize the scores. These normalized weights tell the model how much focus to place on each word. The final output for a token is then a weighted sum of all the value vectors—and this output is called the context vector.

When we make each token attend to every other token within the same sequence, we call it self-attention. In this mechanism, each word learns its relationship with all other words, thereby capturing global dependencies in the sequence.

Masked or Causal Attention

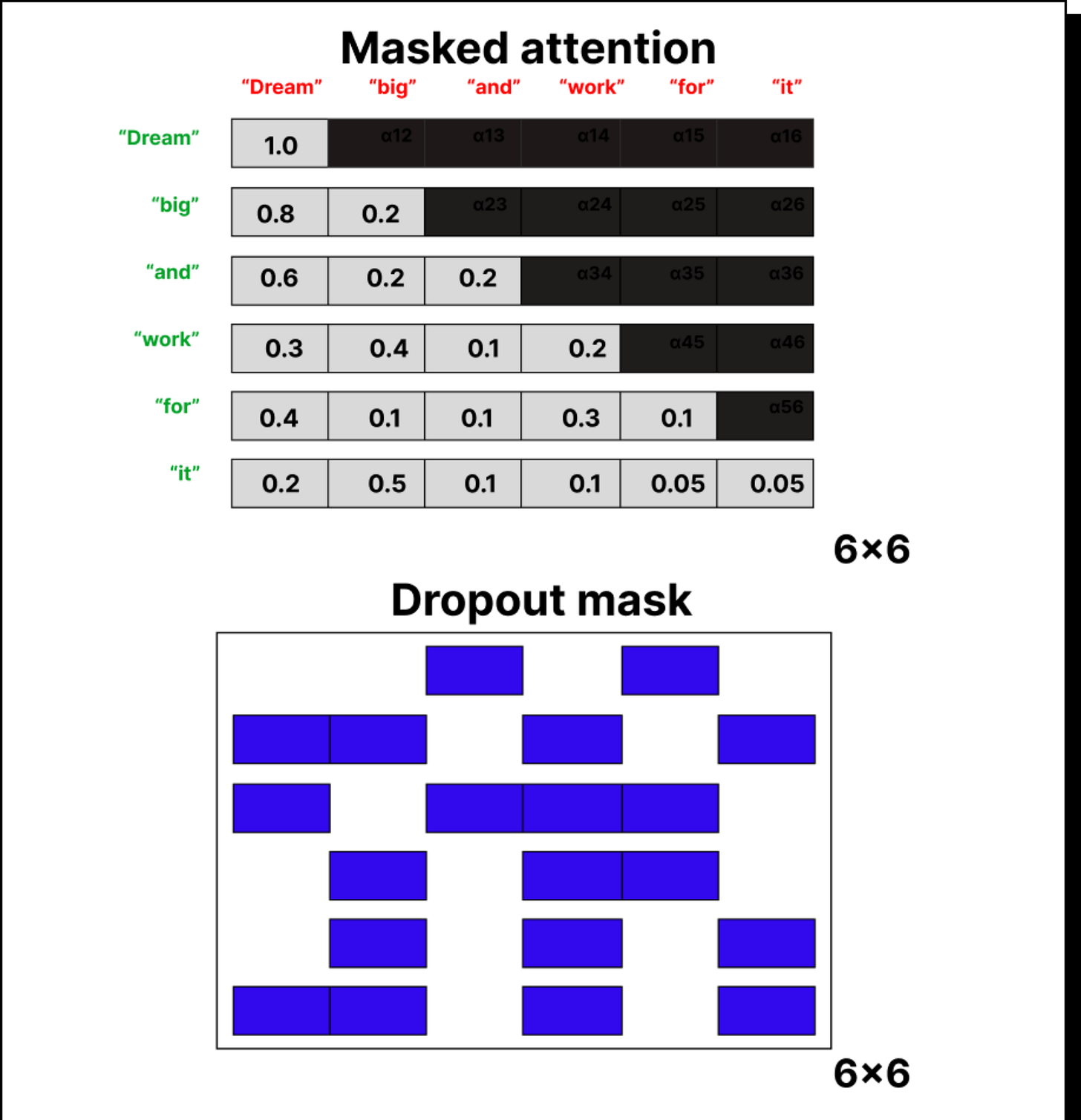
Now, when we are dealing with autoregressive models—where the model predicts the next token based only on the previous ones—we use causal or masked attention. Here we block future tokens by setting their attention weights to zero. To achieve this, we fill the upper triangle of the attention matrix with negative infinity before applying softmax. Because the exponential of negative infinity is zero, these positions get no attention weight. This ensures that the model never cheats by looking into the future.

We also introduce dropout at this stage to prevent overfitting. Randomly setting a portion of attention weights to zero encourages the model to learn more robust patterns instead of memorizing relationships.

Moving from One Head to Many

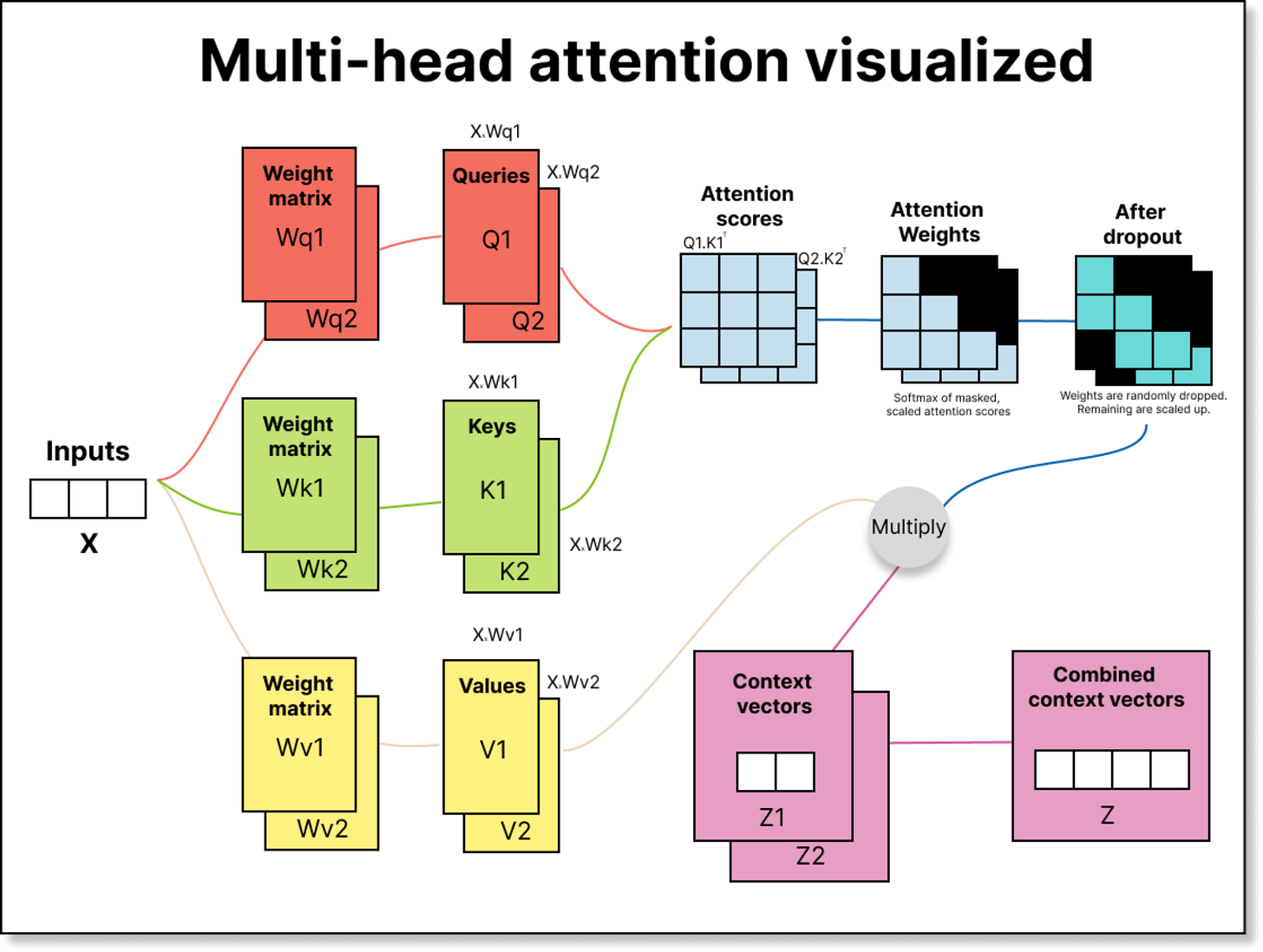
So far, we have discussed single-head attention, where there is just one set of trainable weight matrices—Wq, Wk, and Wv. But the real world is complex, and different parts of an input may capture different kinds of relationships. For example, when reading a sentence, one head might learn grammatical structure, another might focus on sentiment, and a third might capture semantic meaning.

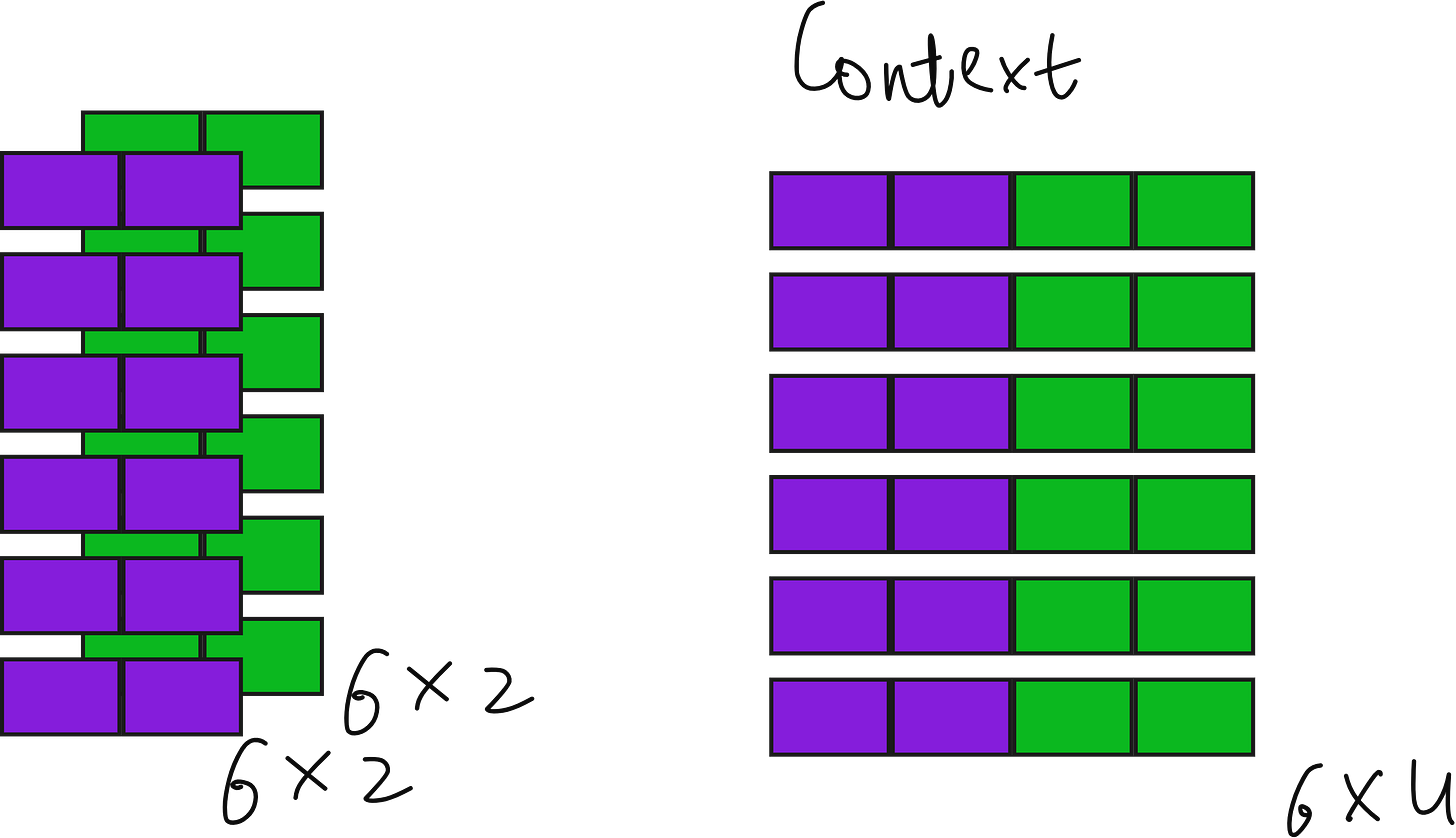
To achieve this diversity, transformers use multiple attention heads. Each head has its own independent Wq, Wk, and Wv matrices. This means each head produces its own set of queries, keys, values, and consequently, its own context vectors. These context vectors are then concatenated to form a single richer representation.

A Numerical Walkthrough

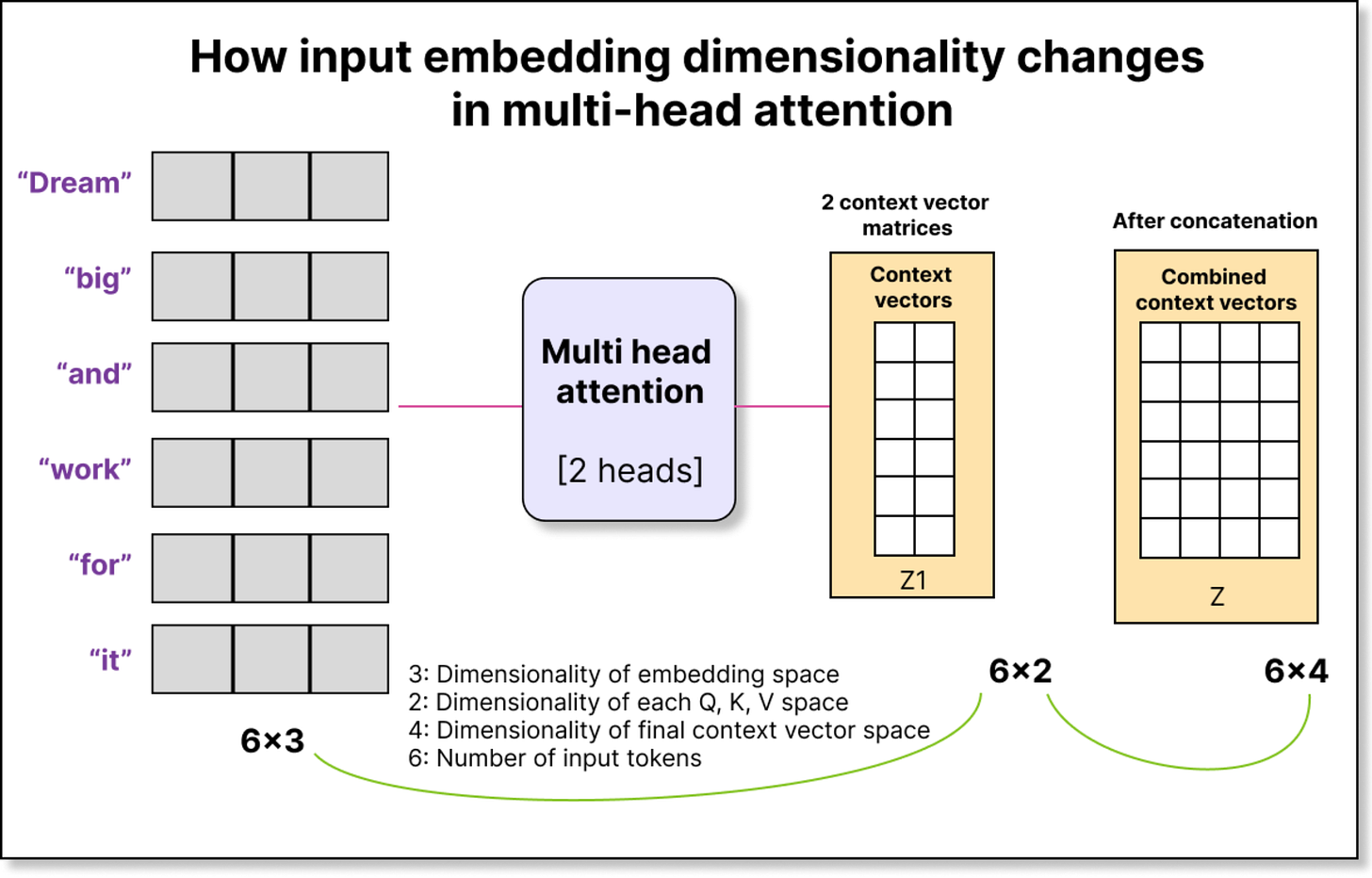
Let us take a simple example. Suppose we have six tokens in our input, each represented by a 3-dimensional embedding. So our input matrix has a shape of 6×3.

Now assume we use two attention heads, and each head projects the input into a 2-dimensional query-key-value space.

For the first head, we multiply the input (6×3) by a trainable weight matrix Wq₁ of shape (3×2) to produce a query matrix Q₁ of shape (6×2).
Similarly, we get K₁ and V₁ for keys and values.
The same happens for the second head, giving us Q₂, K₂, and V₂, all of shape (6×2).

When we perform Q₁ × K₁ᵀ, we get attention scores of shape (6×6) for the first head. The same happens for the second head. After scaling, masking, and applying softmax, we get two sets of attention weights, each (6×6). Multiplying these with the corresponding value matrices (6×2) gives two context vector matrices—each (6×2).

Finally, we concatenate these two matrices along the last dimension to get a combined context matrix of shape 6×4. Each of the six tokens now has a 4-dimensional context vector. With three heads, this would be 6×6; with four heads, 6×8, and so on. The general rule is simple:

Final context dimension = number of heads × dimension per head

Why Multi-Head Attention Works So Well

Each attention head learns to look at the data differently. Since the parameters Wq, Wk, and Wv are all trainable, one head might specialize in short-range dependencies, while another might focus on long-range relationships. Together, they create a more holistic understanding of the input.

This parallelism also allows transformers to process information faster on GPUs, as each head can operate independently and simultaneously. When we combine all the heads, we get a unified representation that is both detailed and diverse in the relationships it captures.

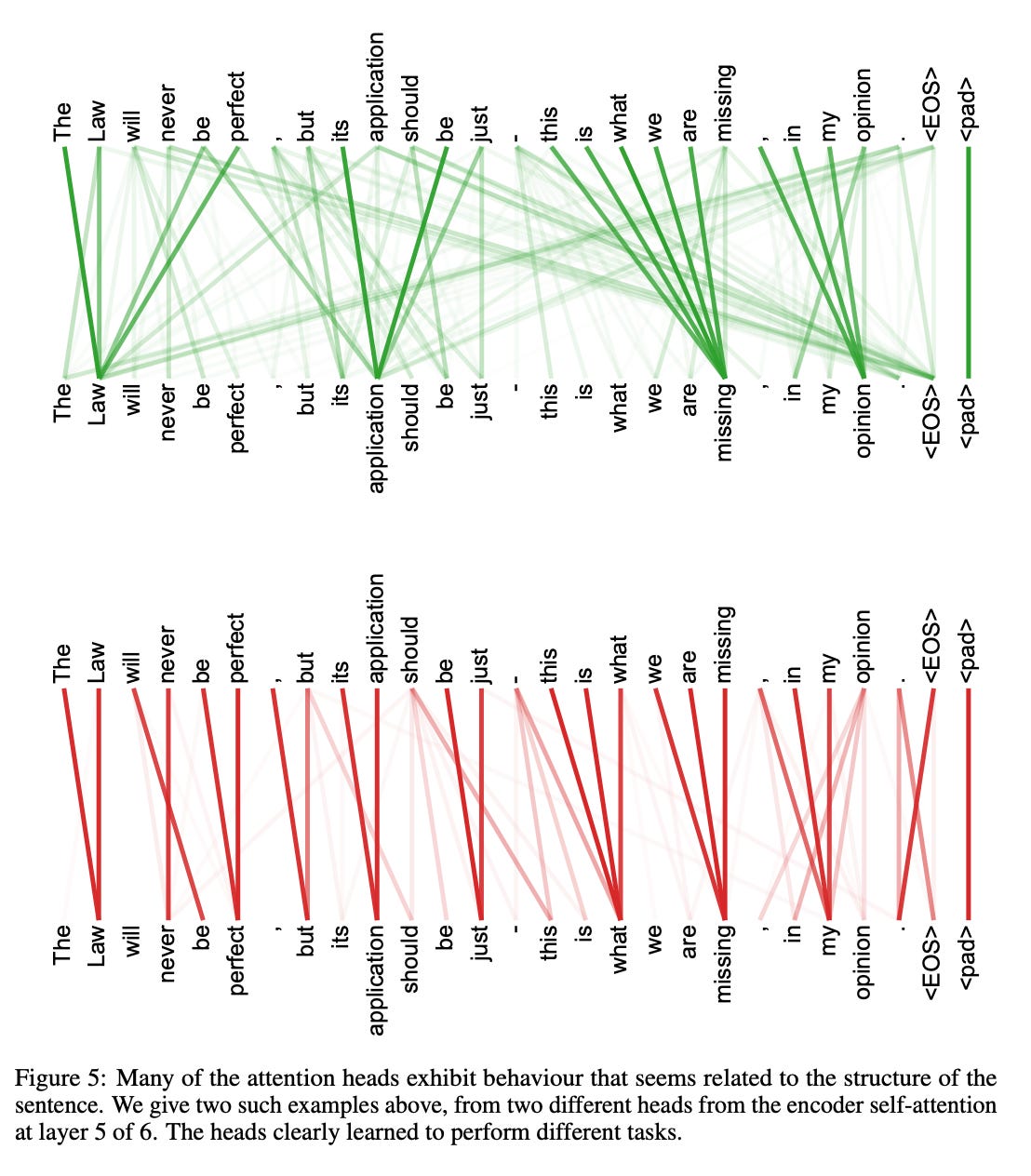
Look at the figure below from “Attention is all you need” paper.

A Peek into the Implementation

In practice, we define a class for causal attention that handles the forward pass. It creates linear transformations for Wq, Wk, and Wv, applies masking, scaling, and softmax, and finally multiplies attention weights with the value matrix to produce context vectors.

For multi-head attention, we simply instantiate this single-head attention multiple times—once for each head—and concatenate their outputs. Although this can be done using for-loops for clarity, modern implementations use a single efficient matrix multiplication that performs all heads in parallel.

In the demonstration, when two heads were used, the final output for each token had four dimensions. With four heads, this became eight dimensions. The code confirmed it by printing the shapes. While the for-loop version is intuitive, it is not computationally efficient, especially when models like GPT-3 have 96 heads per layer and 96 transformer blocks stacked in series.

The Beauty of the Design

The elegance of multi-head attention lies in its simplicity. It does not rely on complex mathematics but on the simple idea of repeating a process several times independently and then combining the results. This division of labor allows the network to see the same input through multiple lenses, leading to richer and more nuanced understanding.

It is this very mechanism that enables GPT models to generate coherent paragraphs, translate languages, and even reason across multiple topics. The same principle, when applied to images in Vision Transformers, allows them to outperform convolutional neural networks on large-scale vision tasks.

Closing Thoughts

If you followed the numerical example step by step, you would have noticed that every operation is just a matrix multiplication followed by scaling and normalization. Nothing magical, yet immensely powerful. This simplicity is what makes transformers elegant and versatile.

I would encourage you to implement this from scratch once, without relying on high-level libraries. Doing so will deepen your intuition and give you the confidence to modify or even innovate new architectures. In the next lecture, we will go a step further and see how to remove the for-loop and implement multi-head attention in a fully vectorized way, just like how large-scale models handle it efficiently on GPUs.