Why do we need "masking" in attention?
Understanding causal or masked self attention
In LLMs, one of the most important yet often misunderstood mechanisms is causal attention, also known as masked self-attention. It is the reason why these models can generate text one word at a time without “peeking” into the future. To truly understand this, we need to start with what attention is and how it evolved into the causal form used in transformers today.
From Input Embeddings to Context Vectors
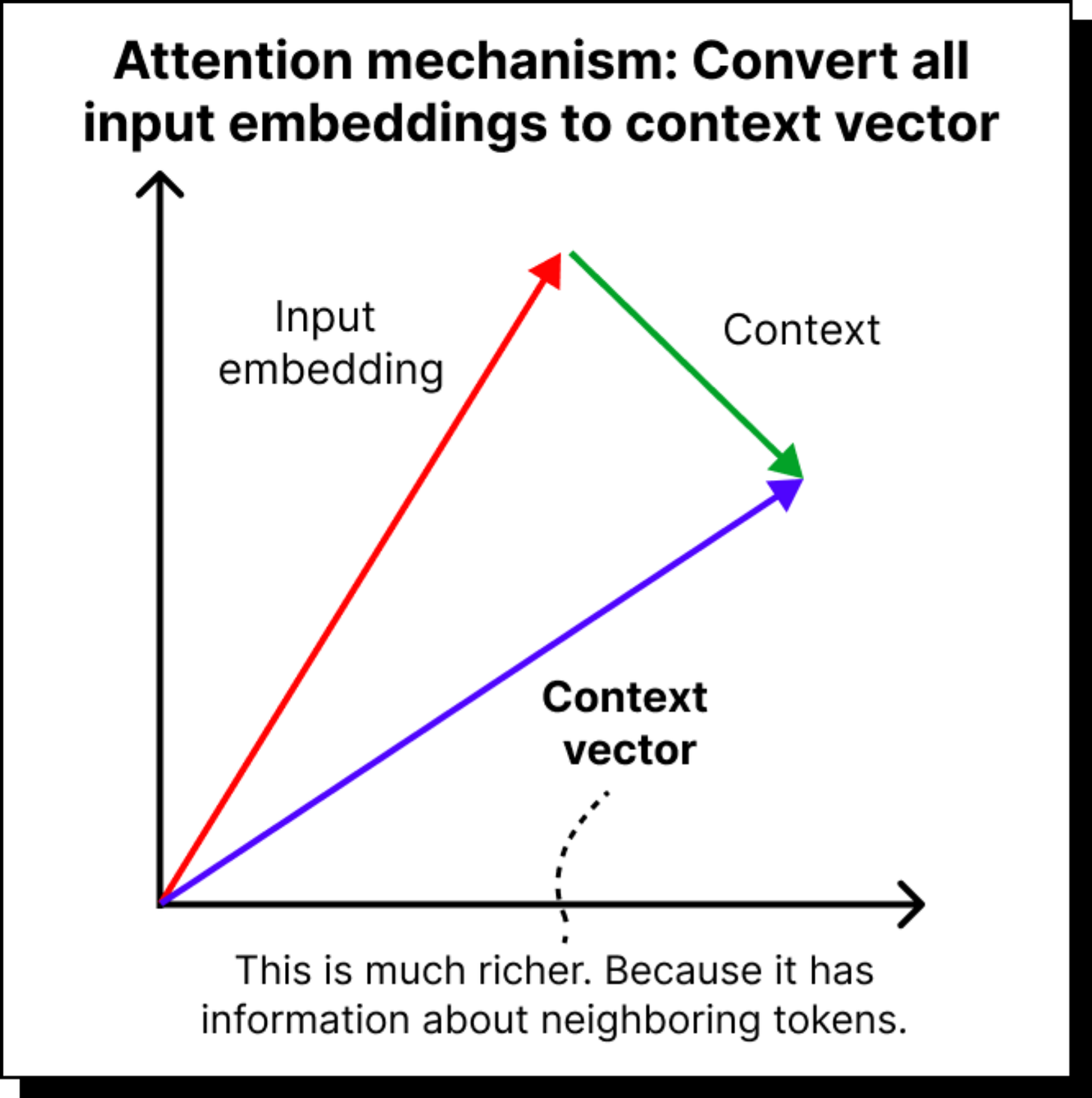
Every token (say, a word or sub-word) that enters a model is converted into a vector called an input embedding. But this embedding, on its own, knows nothing about its neighbors in the sentence. The word cat in “The cat sat on the mat” means little if it doesn’t know that sat and mat are nearby. What we really want is a context vector – a richer representation that captures not just the word itself but its relationship with the surrounding words.
To get this, we use the attention mechanism. It computes how much each token should “attend” to every other token in the sentence. Mathematically, it does this using dot products between vectors. If two vectors are pointing in similar directions in the semantic space, their dot product is large, meaning they are closely related. If they’re orthogonal, the dot product is small, meaning they are unrelated.
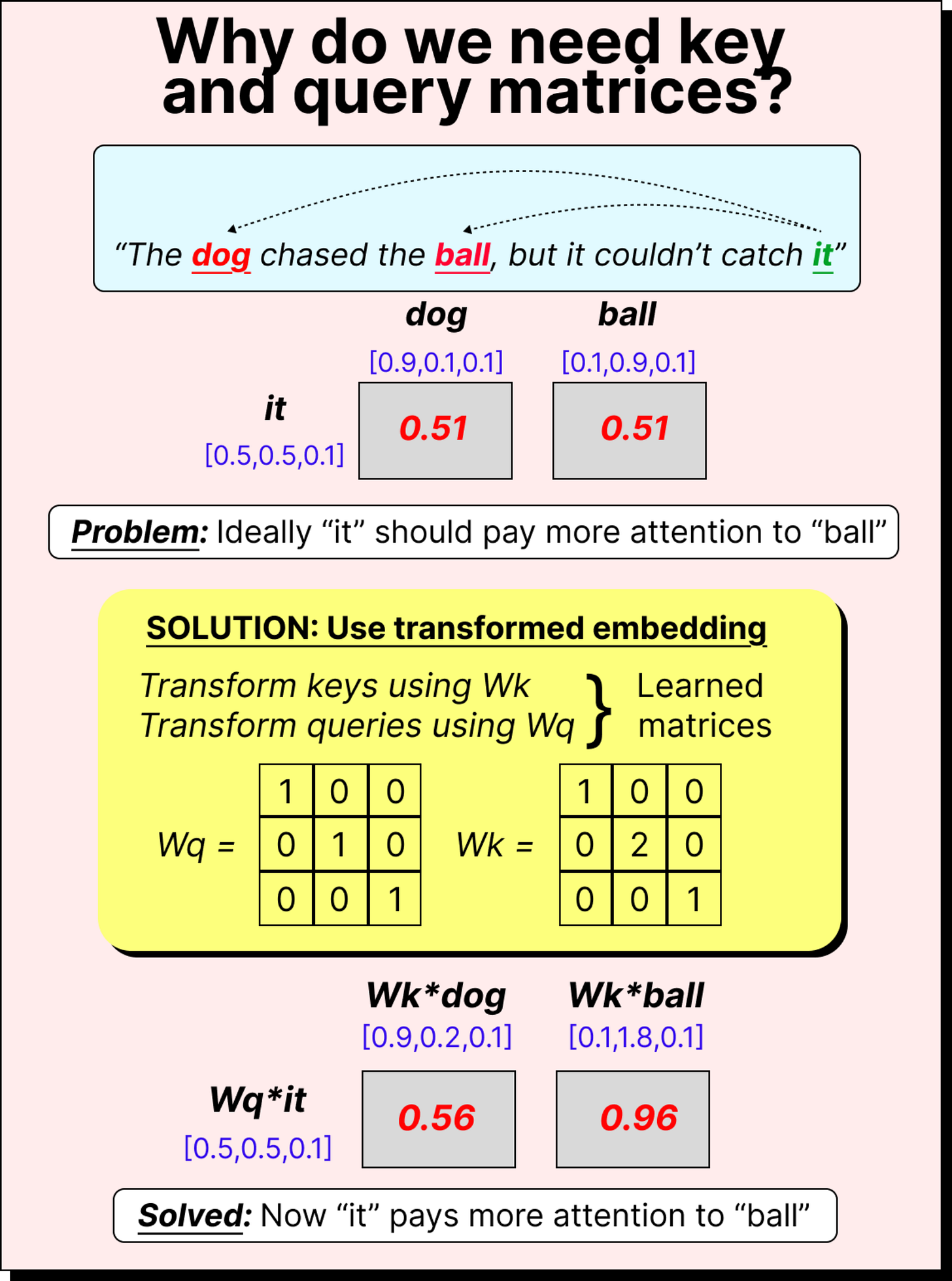
However, using these raw embeddings directly isn’t ideal. The dot products don’t always represent meaningful relationships. For example, in the sentence “The dog chased the ball, but it could not catch it”, the token it should pay more attention to ball than to dog. But direct dot products may fail to show that distinction. To fix this, we introduce three trainable matrices: query (Wq), key (Wk), and value (Wv). These transform embeddings into new spaces where meaningful attention relationships can emerge.
The Core of Self-Attention
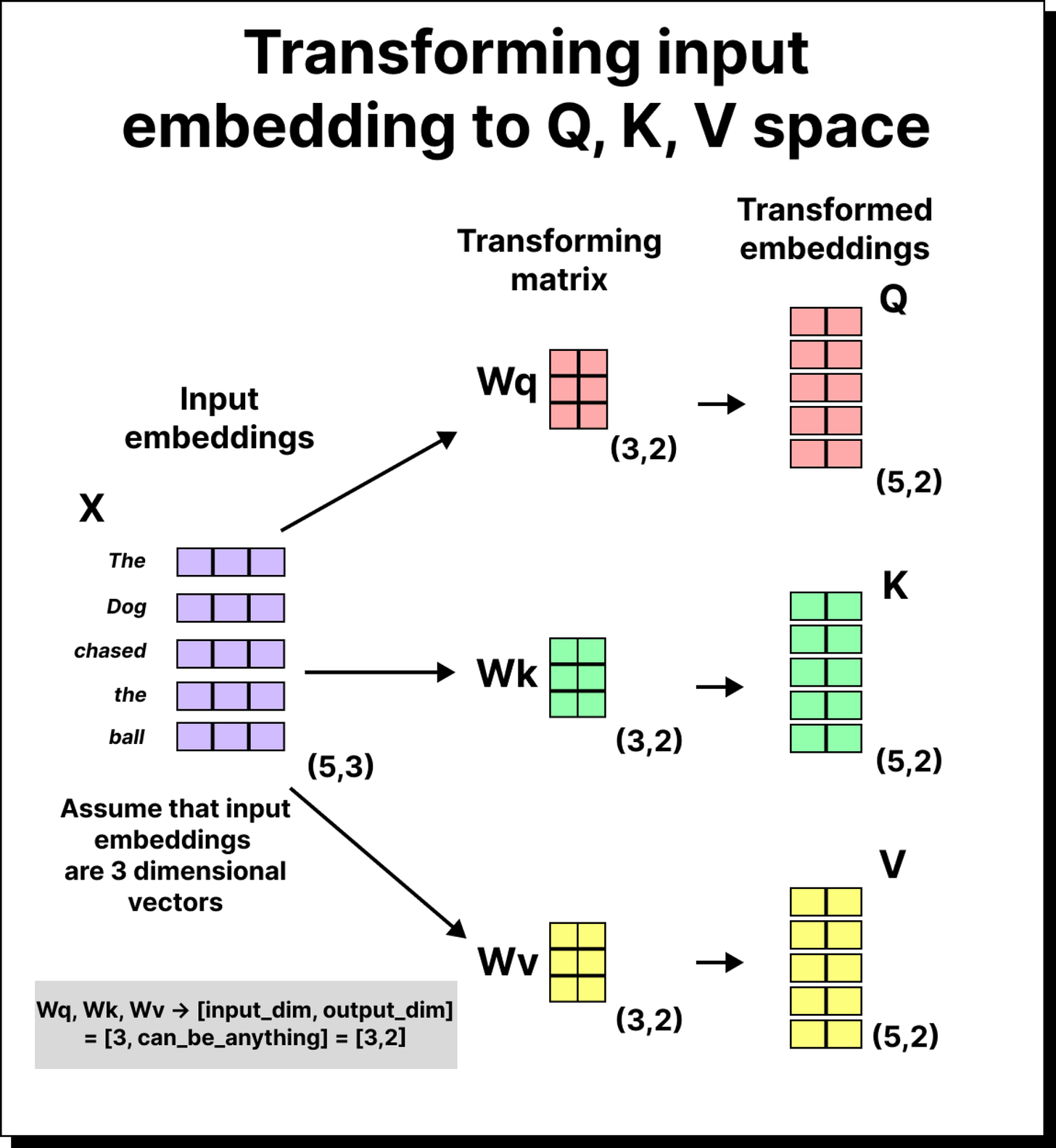
Each token is projected into three spaces:
Query (Q): What am I looking for?
Key (K): What do I contain?
Value (V): What information do I carry?
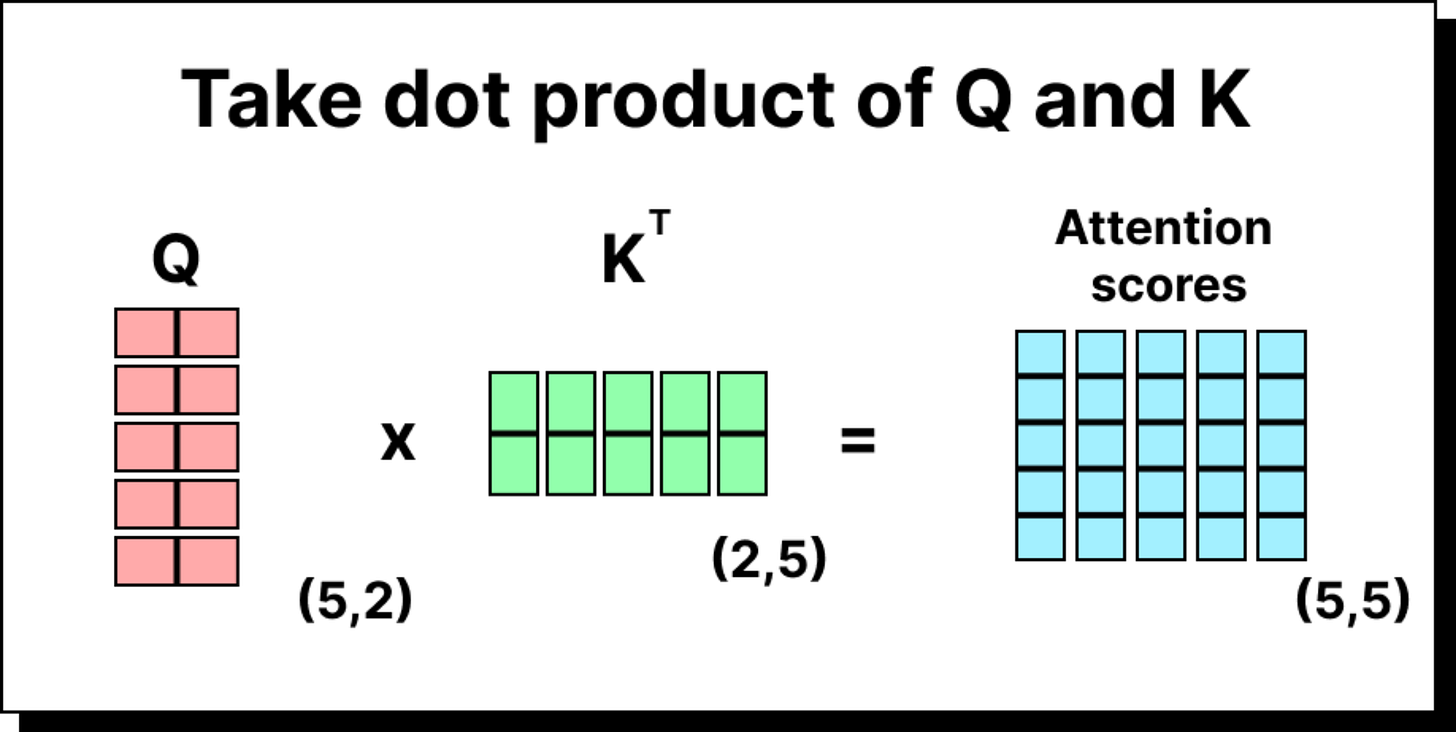
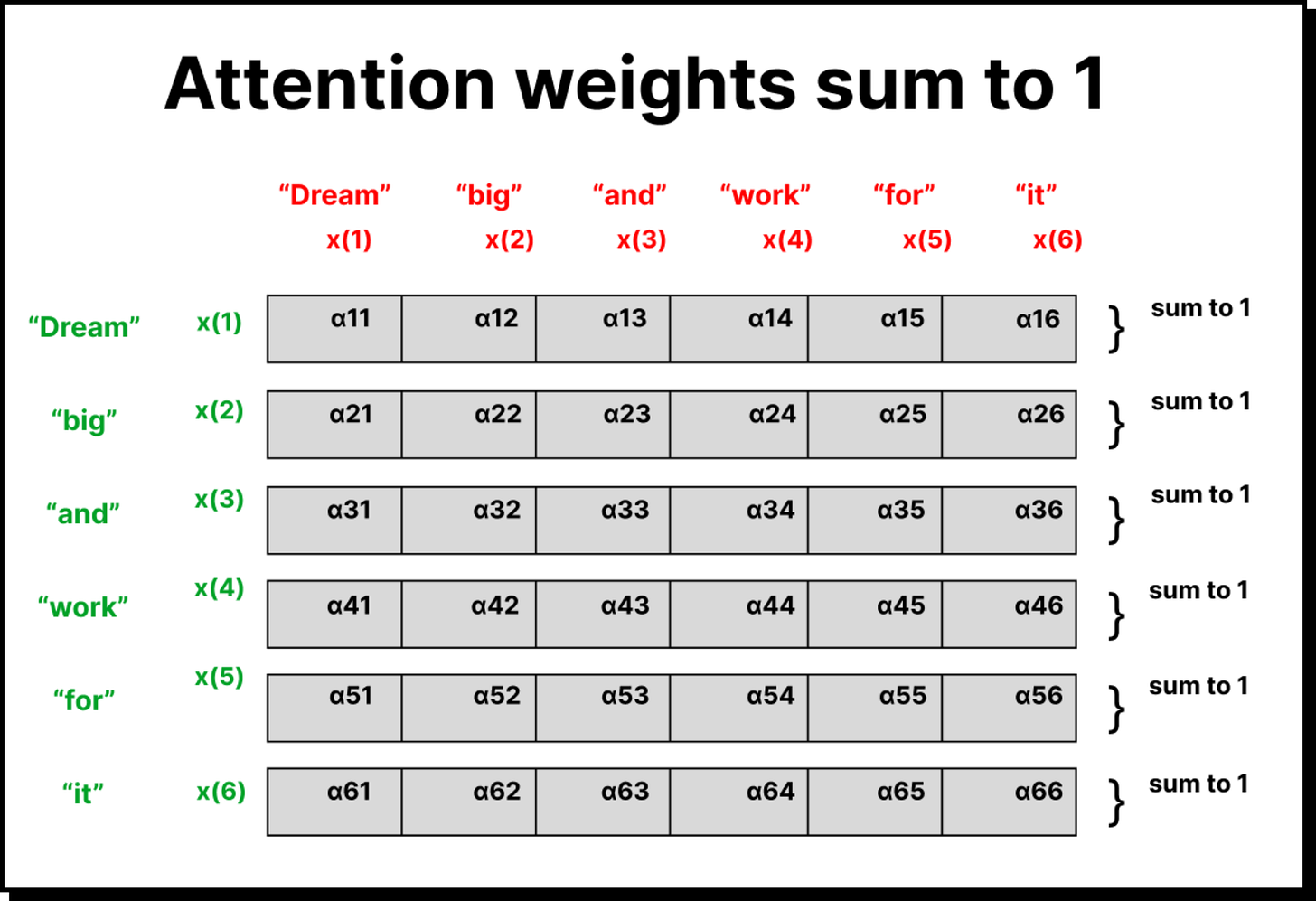
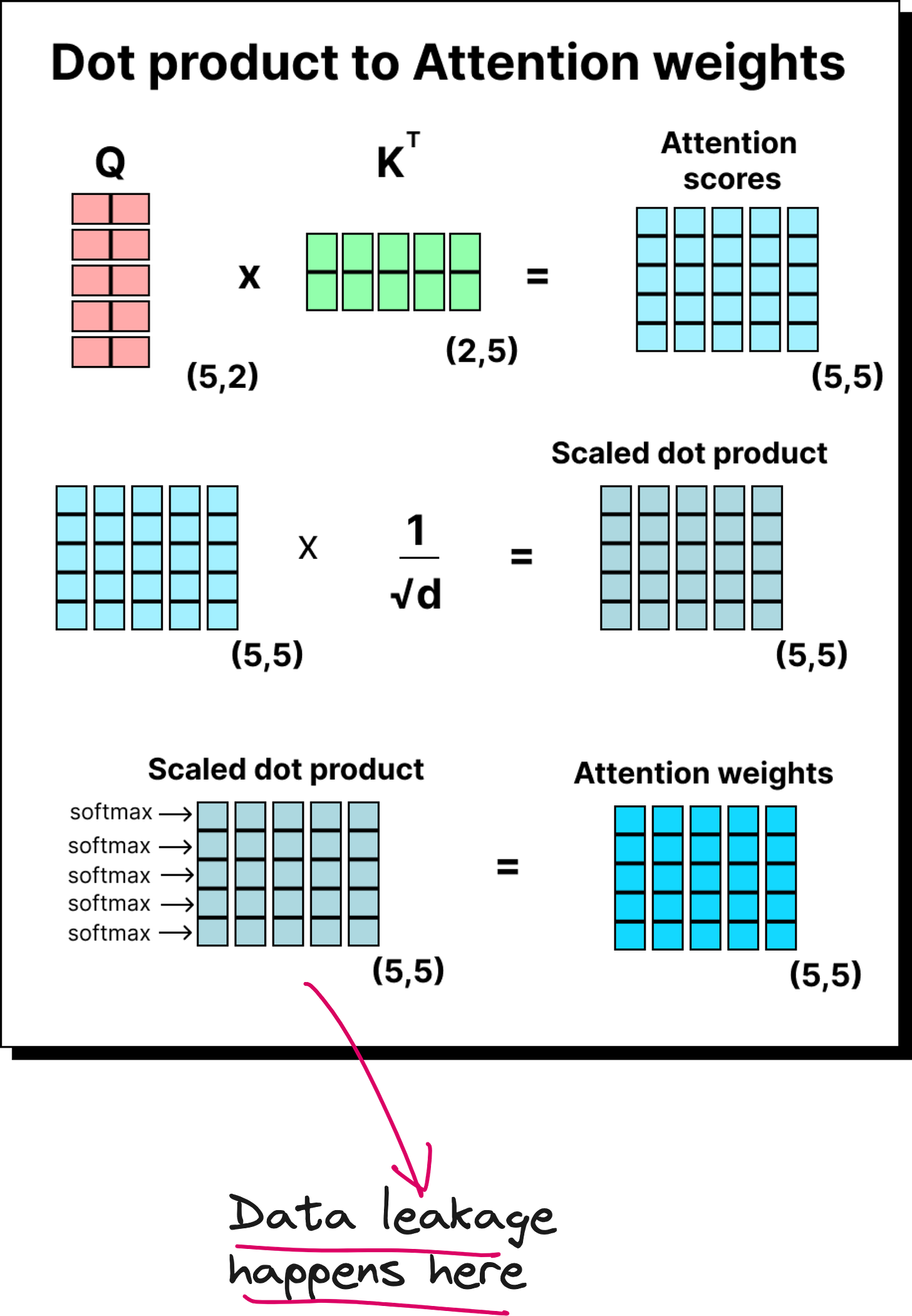
The attention score between two tokens is the dot product of one token’s query and another’s key. We collect these scores into a matrix, scale them by dividing by the square root of the key dimension (to stabilize training), and then normalize each row using the softmax function. The result is a probability-like distribution showing how much attention each token gives to the others.
These are called attention weights, and they are used to compute the final context vectors by taking a weighted sum of the value vectors.
Why Causal Attention Is Needed
So far, this works well when the model has access to the entire sentence. But think about how GPT generates text. It predicts the next word based only on what it has seen so far. It cannot look at future words. When predicting the word big in the sentence “Dream big and work for it”, the model should not know about work, for, or it yet.
That is where causal attention comes in. It ensures that, for each position in the sequence, the model only attends to the tokens before it (and itself), never the tokens ahead. Mathematically, this is done by masking the future positions in the attention matrix.
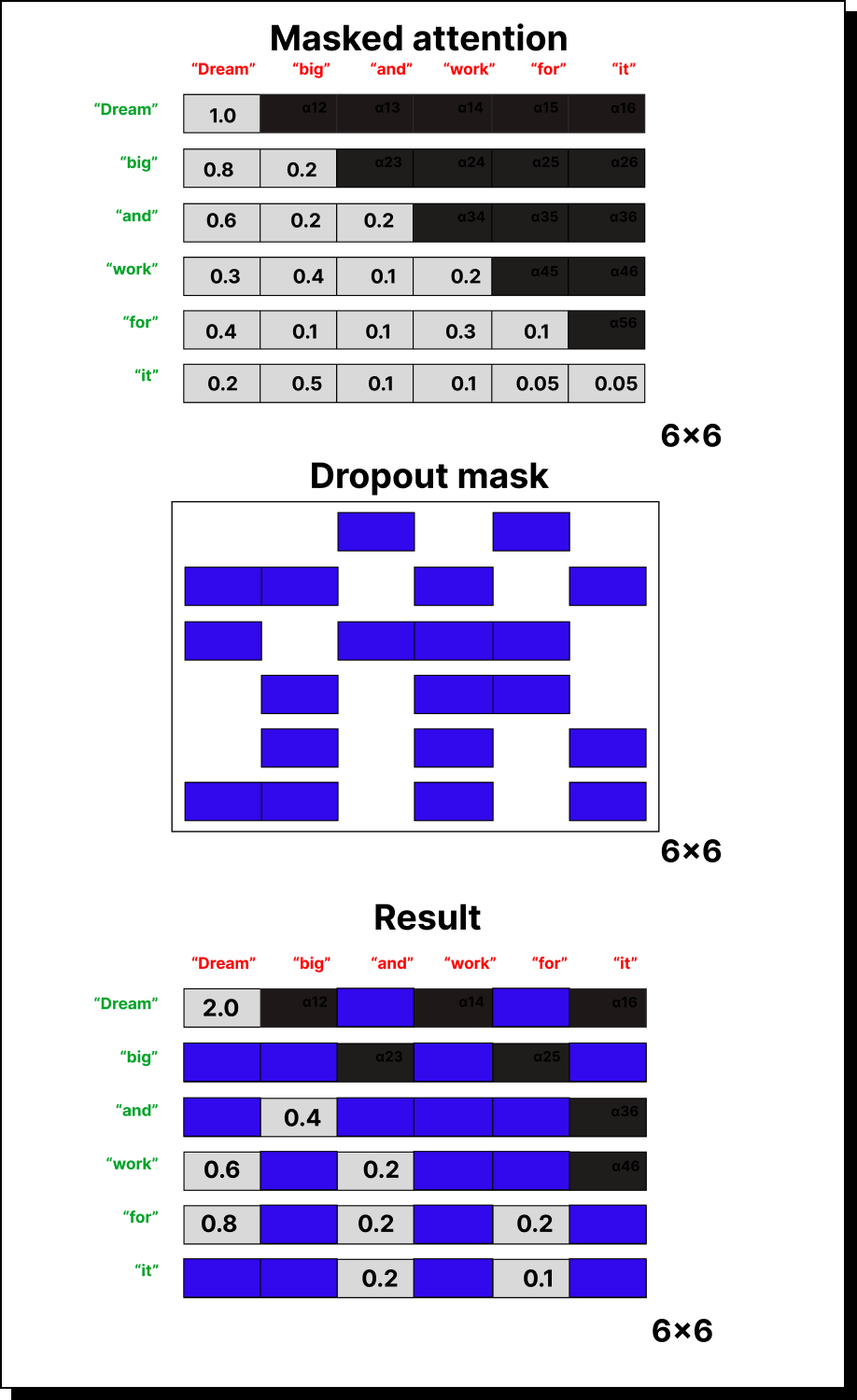
Imagine a 6×6 attention matrix representing six tokens. Everything above the main diagonal (representing future tokens) is replaced with zeros or negative infinity, leaving only the lower triangle active. This effectively tells the model: “You can only look at the past, not the future.”
Masking Before Softmax to Prevent Data Leakage
At first glance, you might think it’s enough to set the upper-triangular elements to zero after computing softmax. But this introduces a subtle error called data leakage. Why? Because softmax involves computing a sum of exponentials of all the numbers in a row. If future tokens are still included in that summation, even as zeroed-out values later, they have already influenced the normalization.
To fix this, we apply the mask before taking softmax. We replace the future elements with negative infinity. When exponentiated, these values become zero, completely removing their influence from the calculation. This ensures the model never sees information from the future while computing attention weights.
For example, if a row contains [2, -∞, -∞], the softmax will yield [1, 0, 0]. This means the current token only attends to itself. Similarly, if the row is [2, 3, -∞], the result after softmax will proportionally distribute attention between the first two tokens and ignore the third entirely. This elegant masking trick guarantees strict causality in attention computation.
Dropout in Attention: Preventing Overdependence
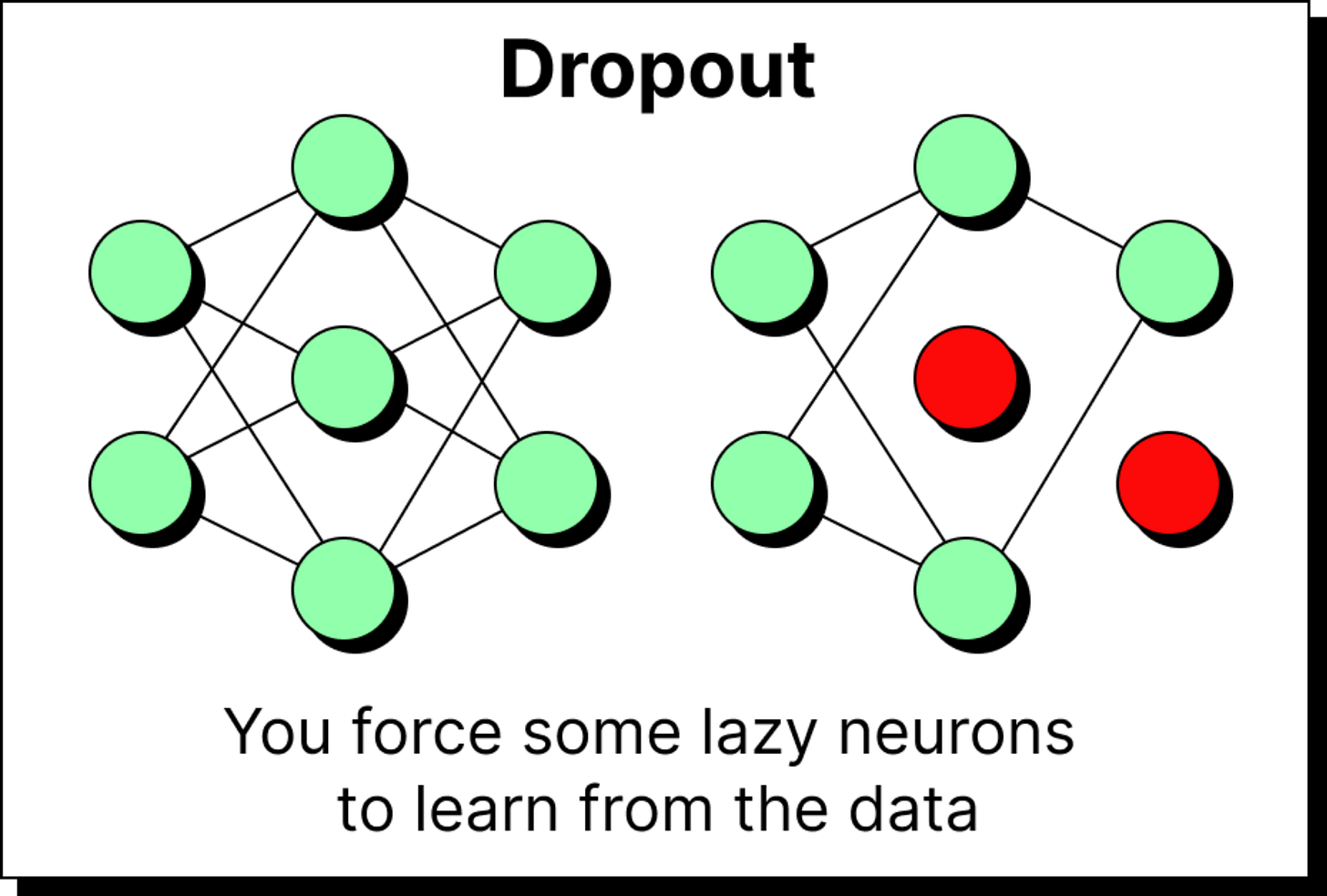
Once masked attention is computed, there’s still one more step before it’s ready for real-world training: dropout. In neural networks, dropout helps prevent overfitting by randomly switching off neurons during training. In the context of attention, dropout prevents the model from becoming too dependent on certain token-to-token relationships.
Suppose ball always attends too strongly to dog in our earlier example. Dropout ensures that some of these attention connections are randomly deactivated during training, forcing the model to learn diverse relationships. When we drop out half of the attention links, the remaining ones are scaled up by a factor of 1 / (1 - p), where p is the dropout probability. This keeps the overall magnitude of the outputs stable even as some connections disappear.
Bringing It All Together
Let’s summarize what we have built:
Start with input embeddings for all tokens.
Transform them into query, key, and value spaces using trainable matrices.
Compute attention scores using dot products between queries and keys.
Mask the future tokens by assigning negative infinity to the upper triangle of the attention matrix.
Apply softmax to obtain normalized attention weights.
Optionally apply dropout to encourage robust learning.
Multiply attention weights with the value matrix to produce context vectors.
These context vectors are then passed to subsequent layers or heads in the transformer model.
The Road Ahead: Multi-Head Attention
What we discussed so far is single-head attention, where one set of query, key, and value matrices is used. In large models like GPT, multiple attention heads run in parallel, each capturing different aspects of the relationships between tokens. Their outputs are concatenated to form the final representation, ensuring that no single head dominates the understanding.
That is the next step in the transformer journey. But by now, you have seen how causal attention ensures that models generate text naturally, one word at a time, without ever breaking the temporal flow of language.
Final Thoughts
The beauty of causal attention lies in its simplicity. By masking out future tokens, the model mirrors how humans think while writing – we can only build upon what we have written so far. The introduction of this simple yet powerful concept transformed the way neural networks handle sequential data, replacing complex recurrent architectures with something that is elegant, scalable, and mathematically transparent.
In the next part of this series, we will look into multi-head self-attention – the mechanism that allows transformers to look at the same sentence from multiple perspectives simultaneously, forming the true backbone of GPT and Vision Transformers alike.