What is a teacher student model in Deep Learning?
How does its loss function actually work?
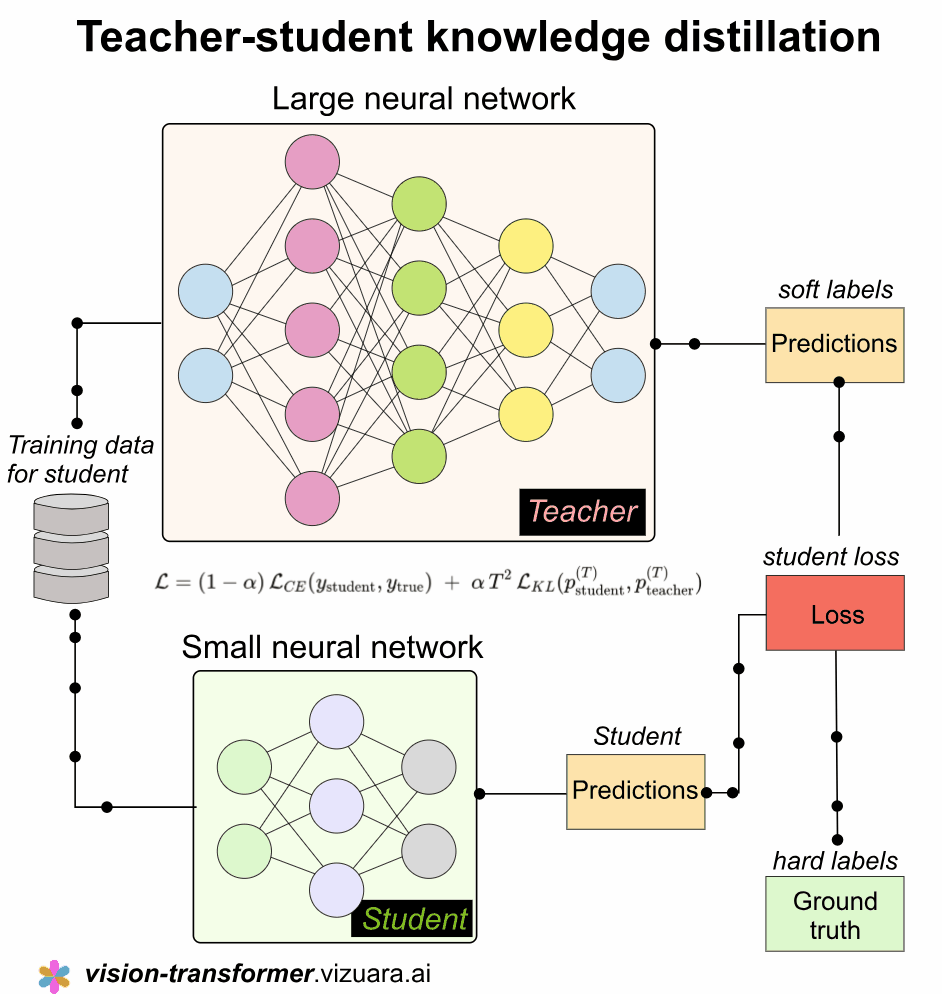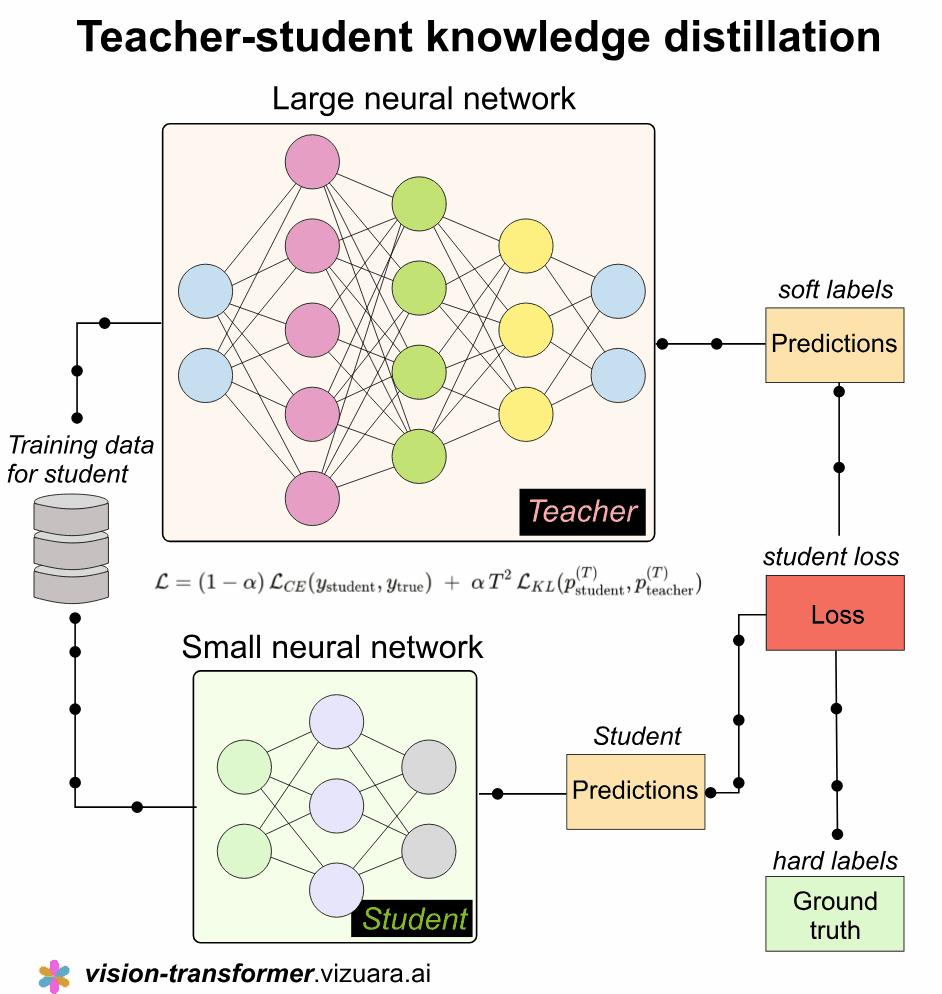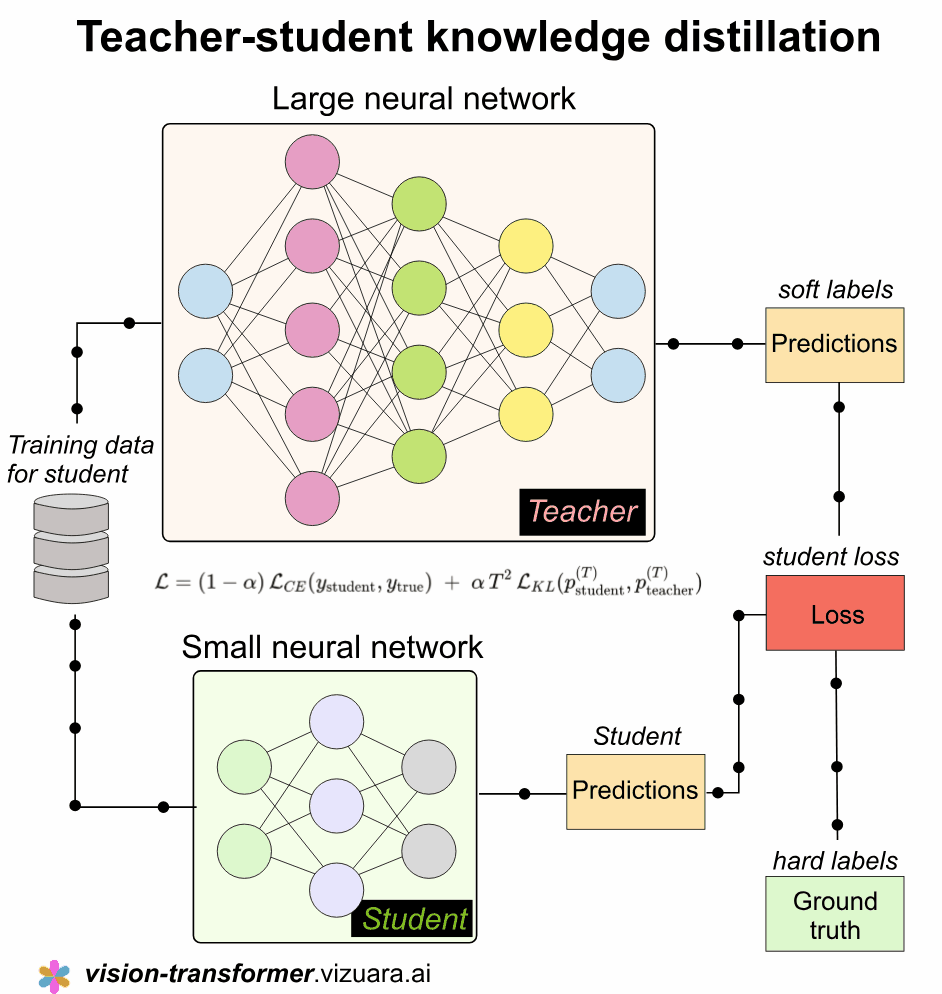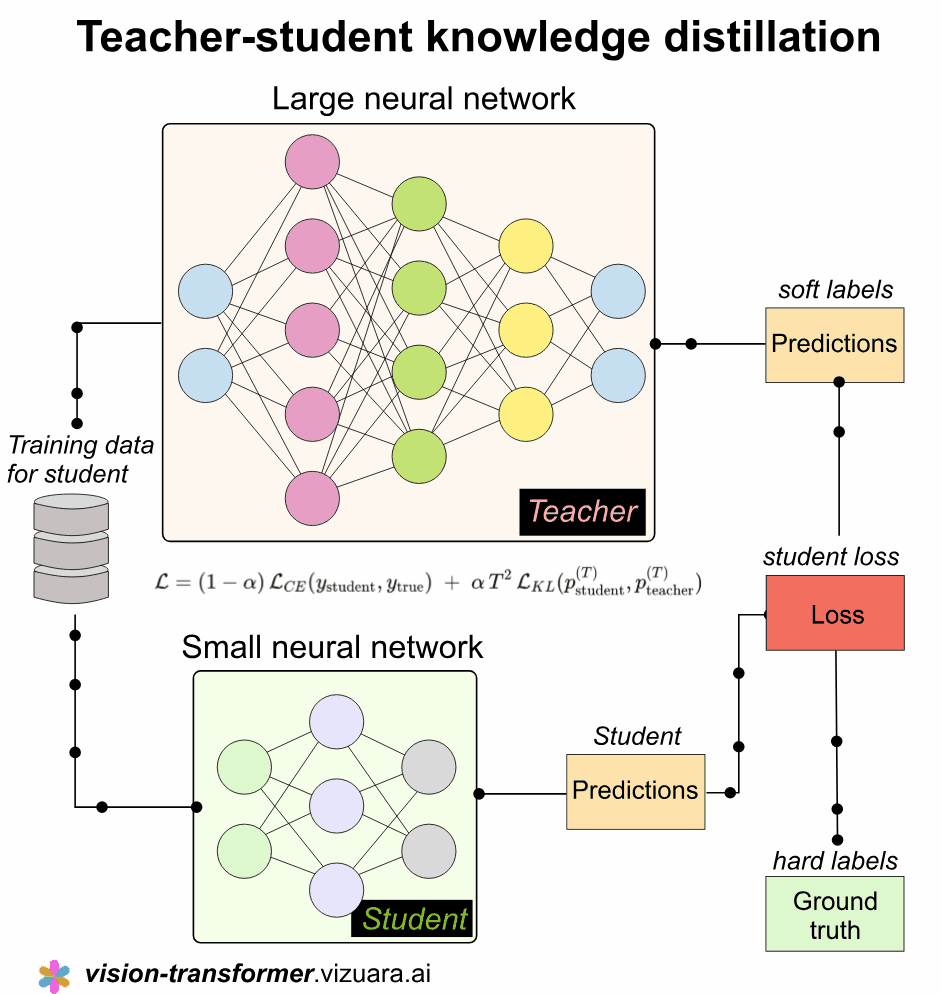
When we talk about a teacher student framework in deep learning, we are essentially describing a very intuitive learning arrangement where a large and highly trained model guides a smaller model so that the smaller one can pick up not only the final answers but also the nuanced patterns that the bigger model has learned over time, and this simple idea has become extremely important because it allows us to deploy compact models that perform surprisingly well even on devices with very limited compute.
Teacher model
The teacher model is usually a heavy network trained on massive datasets, which means it does not simply say that an image is a cat or a dog but instead gives a smooth distribution such as seventy percent cat, twenty percent fox, and ten percent dog, and this rich distribution captures relationships between classes in a way that hard labels can never capture, so the teacher essentially passes down its internal understanding to the student.
Student model
The student model, which is usually smaller, lighter, and much faster, learns from two sources at the same time, and this is an important idea because the student is not abandoned with only the hard labels but is guided by the softer and more informative probabilities of the teacher, which improves its generalization far more than standard supervised learning would.
Loss function
The entire process is implemented using a combined loss function that blends two objectives, and the structure of this combined loss is quite elegant because it ensures that the student respects the ground truth while also absorbing the deeper knowledge present in the teacher’s probability distribution.
The overall loss function looks like this:
and this single expression captures the entire philosophy of knowledge distillation, where α controls how much importance we place on the teacher, T is the temperature that smooths the teacher’s predictions, and the two losses work hand in hand to shape the student’s learning curve.
The KL divergence is written as:
and this formulation ensures that the student is encouraged to match the structure of the teacher’s beliefs rather than just its top prediction.
Temperature
The temperature T is extremely important because a high temperature softens the logits and reveals how the teacher distributes probability mass across classes, and multiplying by T squared compensates for the smaller gradients that occur when temperature increases, ensuring that the training remains stable and effective.
This loss function has become a foundational tool not only in vision tasks but also in transformers for language and multimodal learning, and whenever we want a compact model that behaves almost like a larger model, this teacher student formulation becomes a natural and highly practical strategy.




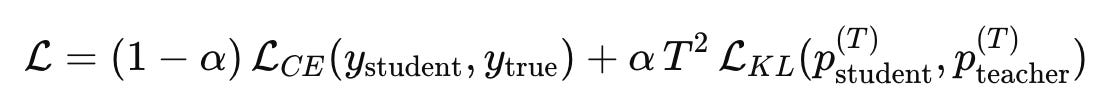
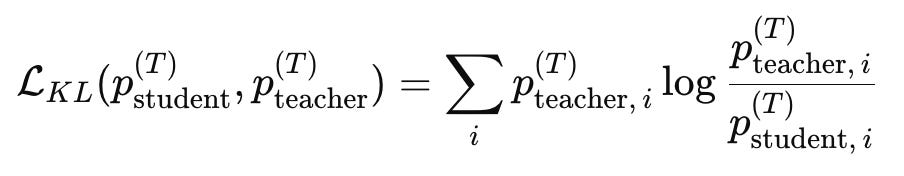
This article comes at the perfect time! I was literally just pondering how to get these powerful models onto more accessible devices. Your breakdown of the teacher-student framework, especially the soft labels, is briliant. It totally connects with your previous piece on knowledge distillation. Such a smart, clear explanation!