Stochastic Gradient Descent from Scratch

With a recap of vanilla/normal/batch gradient descent

Optimization in machine learning is all about finding that sweet spot—a set of parameters that minimizes error. While Gradient Descent laid the foundation for this, its practical limitations called for an upgrade: Stochastic Gradient Descent (SGD). Let’s dive deep into how SGD works and why it’s a game-changer. We will also implement Stochastic Gradient from scratch at the end of this article.

A quick recap on vanilla gradient descent

Recap of Gradient Descent and Its Shortcomings

What Is Gradient Descent?

Gradient Descent is an iterative optimization algorithm used to minimize a loss function L(θ). At each step, it updates the model parameters θ by moving in the direction opposite to the gradient of the loss function with respect to θ:

\(\theta = \theta - \eta \nabla L(\theta) \)

Here:

• ∇L(θ): Gradient of the loss function.

• η: Learning rate (step size).

Key Properties:

1. It computes the gradient over the entire dataset at each step.

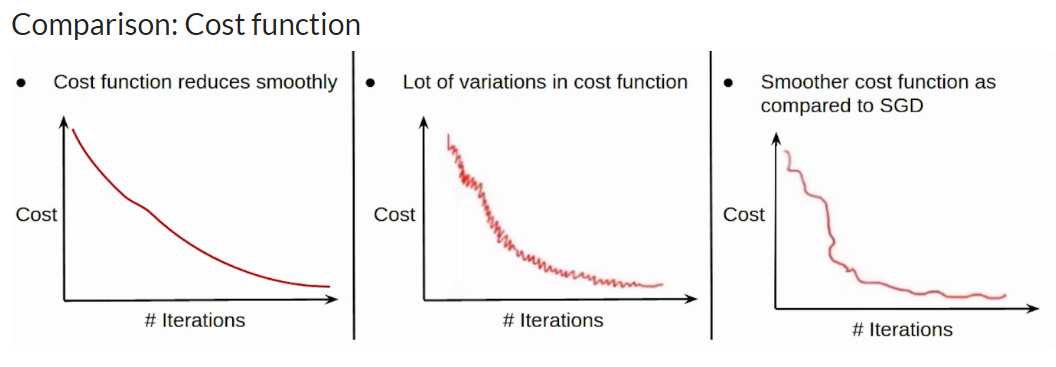
2. Guarantees a smooth and steady descent towards the minimum of L(θ)

Shortcomings of Gradient Descent

1. Computational Overhead: Calculating the gradient over the entire dataset is computationally expensive for large datasets.

   • Example: For a dataset with N samples, computing the gradient requires N operations per update.

2. Slow Convergence: Gradient Descent can take small, steady steps and struggle with large datasets or complex loss landscapes.

3. Local Minima or Saddle Points: It may get stuck in a local minimum or wander in a flat saddle region, delaying convergence.

These limitations led to the development of Stochastic Gradient Descent, which makes optimization faster and more flexible.

NOTE: The “normal” gradient descent is also called as vanilla gradient descent or batch gradient descent (BGD). Batch because the parameter update is calculated with respect to all data points in the batch.

Stochastic Gradient Descent: Breaking It Down

What Is SGD?

Instead of calculating the gradient over the entire dataset, SGD estimates the gradient using just one data point at a time. This introduces randomness (or "stochasticity") into the optimization process, allowing faster and noisier updates.

The SGD update rule is:

\(\theta = \theta - \eta \nabla L(\theta; x_i, y_i) \)

Here:

• (xi,yi): A single data point chosen randomly from the dataset.

• ∇L(θ;xi,yi): Gradient of the loss function with respect to θ for this data point.

Advantages of SGD

1. Speed: Faster updates as only a single data point is used, making it ideal for large datasets.

2. Escaping Local Minima: The noise introduced by random updates helps SGD escape local minima and explore the parameter space.

3. Scalability: Works well for streaming data or online learning, where data arrives in small batches.

Challenges of SGD

1. Noisy Updates: Individual gradients can vary significantly, leading to fluctuations in convergence.

2. Slower Convergence to the Exact Minimum: Due to noise, SGD may hover near the minimum rather than converging precisely.

3. Sensitivity to Learning Rate: Choosing an appropriate η is critical; too high causes divergence, too low slows down learning.

Left: Vanilla gradient descent, middle: Stochastic gradient descent, right: mini-batch gradient descent

For big dataset, there is a huge difference in the time required for executing the code between BGD and SGD. SGD is much faster.

Small dataset: 1000 points. Large dataset: 10 million points.

Code implementation of Stochastic v/s Batch Gradient Descent

import numpy as np
import matplotlib.pyplot as plt
import time

def generate_data(num_samples):
    np.random.seed(42)
    X = np.random.rand(num_samples, 1) * 10  # Features
    y = 3 * X + 7 + np.random.randn(num_samples, 1)  # Target with some noise
    return X, y

def compute_loss(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

def batch_gradient_descent(X, y, epochs, lr=0.01 ):
    m, n = X.shape
    X = np.c_[np.ones((m, 1)), X]  # Add bias term
    theta = np.random.randn(n + 1, 1)
    losses = []

    for epoch in range(epochs):
        predictions = X.dot(theta)
        errors = predictions - y
        gradients = 2 / m * X.T.dot(errors)
        theta -= lr * gradients
        loss = compute_loss(y, predictions)
        losses.append(loss)

    return theta, losses

def stochastic_gradient_descent(X, y,epochs, lr=0.01 ):
    m, n = X.shape
    X = np.c_[np.ones((m, 1)), X]  # Add bias term
    theta = np.random.randn(n + 1, 1)
    losses = []

    for epoch in range(epochs):
        random_index = np.random.randint(m)
        xi = X[random_index:random_index + 1]
        yi = y[random_index:random_index + 1]
        predictions = xi.dot(theta)
        errors = predictions - yi
        gradients = 2 * xi.T.dot(errors)
        theta -= lr * gradients
        epoch_loss += compute_loss(yi, predictions)
        losses.append(epoch_loss)

    return theta, losses

small_dataset_size = 1000
large_dataset_size = 10000000

X_small, y_small = generate_data(small_dataset_size)
X_large, y_large = generate_data(large_dataset_size)

#for small dataset
start_time = time.time()
theta_bgd_small, losses_bgd_small = batch_gradient_descent(X_small, y_small, epochs=50)
time_bgd_small = time.time() - start_time

#for large dataset
start_time = time.time()
theta_bgd_large, losses_bgd_large = batch_gradient_descent(X_large, y_large, epochs=50)
time_bgd_large = time.time() - start_time

#for small dataset
start_time = time.time()
theta_sgd_small, losses_sgd_small = stochastic_gradient_descent(X_small, y_small, epochs=50)
time_sgd_small = time.time() - start_time

#for large dataset
start_time = time.time()
theta_sgd_large, losses_sgd_large = stochastic_gradient_descent(X_large, y_large, epochs=50)
time_sgd_large = time.time() - start_time

print("Batch Gradient Descent (Small Dataset): Time = {:.4f}s, Final Loss = {:.4f}".format(time_bgd_small, losses_bgd_small[-1]))
print("Batch Gradient Descent (Large Dataset): Time = {:.4f}s, Final Loss = {:.4f}".format(time_bgd_large, losses_bgd_large[-1]))
print("Stochastic Gradient Descent (Small Dataset): Time = {:.4f}s, Final Loss = {:.4f}".format(time_sgd_small, losses_sgd_small[-1]))
print("Stochastic Gradient Descent (Large Dataset): Time = {:.4f}s, Final Loss = {:.4f}".format(time_sgd_large, losses_sgd_large[-1]))

plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(losses_bgd_small, label="Batch GD (Small Dataset)")
plt.plot(losses_sgd_small, label="Stochastic GD (Small Dataset)")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.title("Small Dataset")

plt.subplot(1, 2, 2)
plt.plot(losses_bgd_large, label="Batch GD (Large Dataset)")
plt.plot(losses_sgd_large, label="Stochastic GD (Large Dataset)")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.title("Large Dataset")

plt.tight_layout()
plt.show()

Conclusion: For big datasets, SGD is faster. It may or may not give a lower loss depending on the number of epochs.