Let us implement a simplified self attention
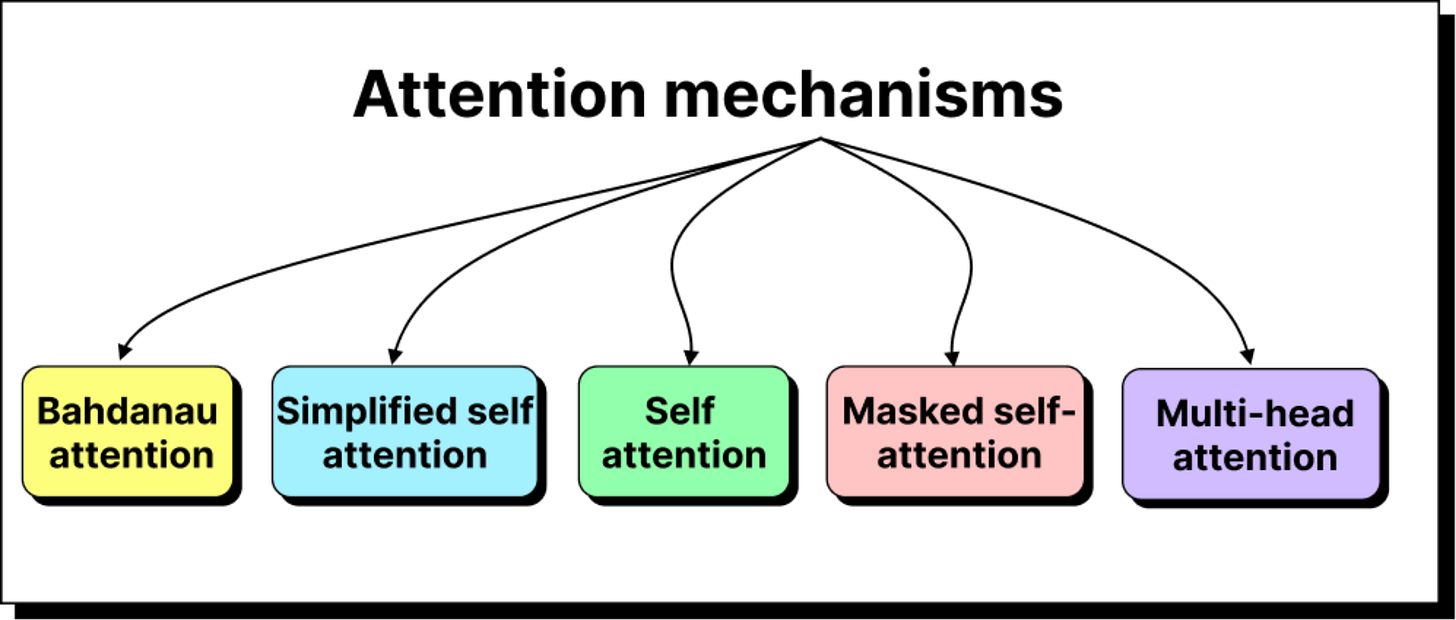
Introduction to attention mechanism
From Recurrent Networks to Self-Attention: How Machines Learn to Focus
In the earlier lectures, we explored the journey of neural machine translation and saw how the encoder-decoder architecture based on recurrent neural networks formed the backbone of early language models. These models were remarkable at handling short sentences, but they struggled when it came to long and complex sentences where words separated by distance still carried meaning for one another. It is in solving this challenge that the concept of attention was born, a simple yet powerful idea that changed the course of natural language processing forever.
The Problem of Long-Range Dependency
Imagine a sentence such as “The teacher who was teaching a difficult concept to the students smiled.”
If we try to make a model understand who smiled in this sentence, the correct answer is the teacher, not the students. But there is a long gap between the word teacher at the beginning and smiled at the end. This kind of long-range dependency is very difficult for a recurrent neural network to capture because, in the traditional encoder-decoder setup, the entire sentence is squeezed into a single context vector that must carry all the information. This puts immense pressure on the model to remember everything, and inevitably, it starts forgetting details as sentences grow longer.
Bahdanau’s Breakthrough: Letting the Decoder Look Back
In 2014, Bahdanau and colleagues proposed a clever modification. Instead of forcing the decoder to rely only on one compressed context vector, they allowed it to access all the hidden states of the encoder. Every output token could now selectively attend to the most relevant parts of the input sequence. For instance, when predicting the French equivalent of “smiled,” the decoder could give more importance to the hidden state corresponding to “teacher” than to “students.”
Mathematically, this attention is represented through weights (α) that determine how much importance each encoder state receives while generating a particular decoder output. This mechanism came to be known as Bahdanau attention. It was the first time neural networks began to “look back” intelligently rather than remembering blindly.
The Leap to Self-Attention
Bahdanau’s method worked beautifully for translation tasks involving two sequences — one in the input language and one in the output. But what if we wanted a model to focus within a single sequence itself, such as when understanding the relationship between words in the same sentence?
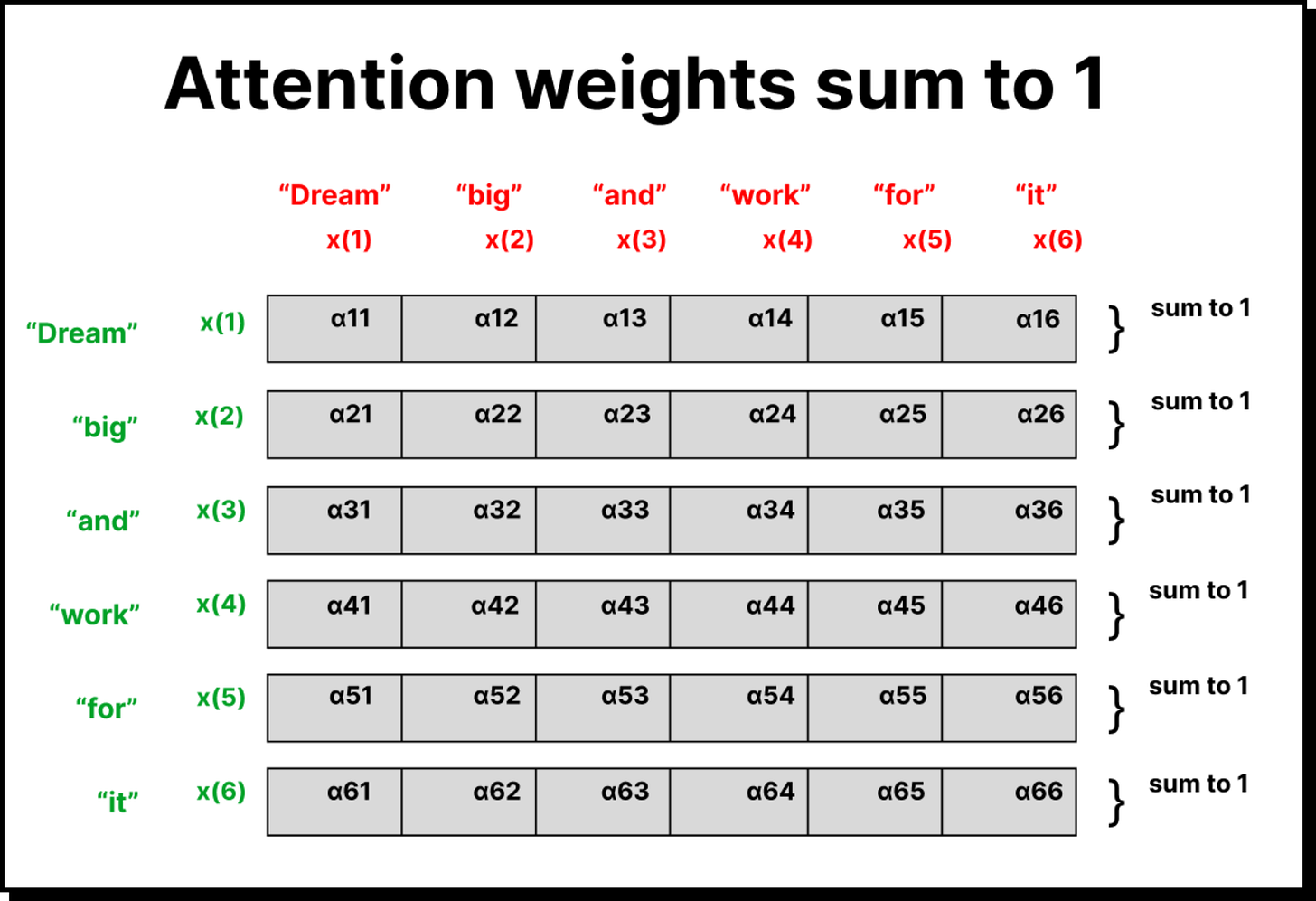
This gave rise to self-attention, where each word in a sentence decides how much attention to pay to every other word in the same sentence, including itself. The idea is that words influence one another’s meaning, and by quantifying that influence, we can represent context far better than before. In this setup, the attention matrix becomes square because the number of words in the input and output sequences are the same.
From Words to Vectors: The Language of Numbers
Words in a machine are not stored as text but as numerical vectors in an n-dimensional space. These are called word embeddings. Similar words, such as “apple” and “orange,” tend to lie closer in this semantic space, while unrelated words like “dog” and “apple” are far apart.
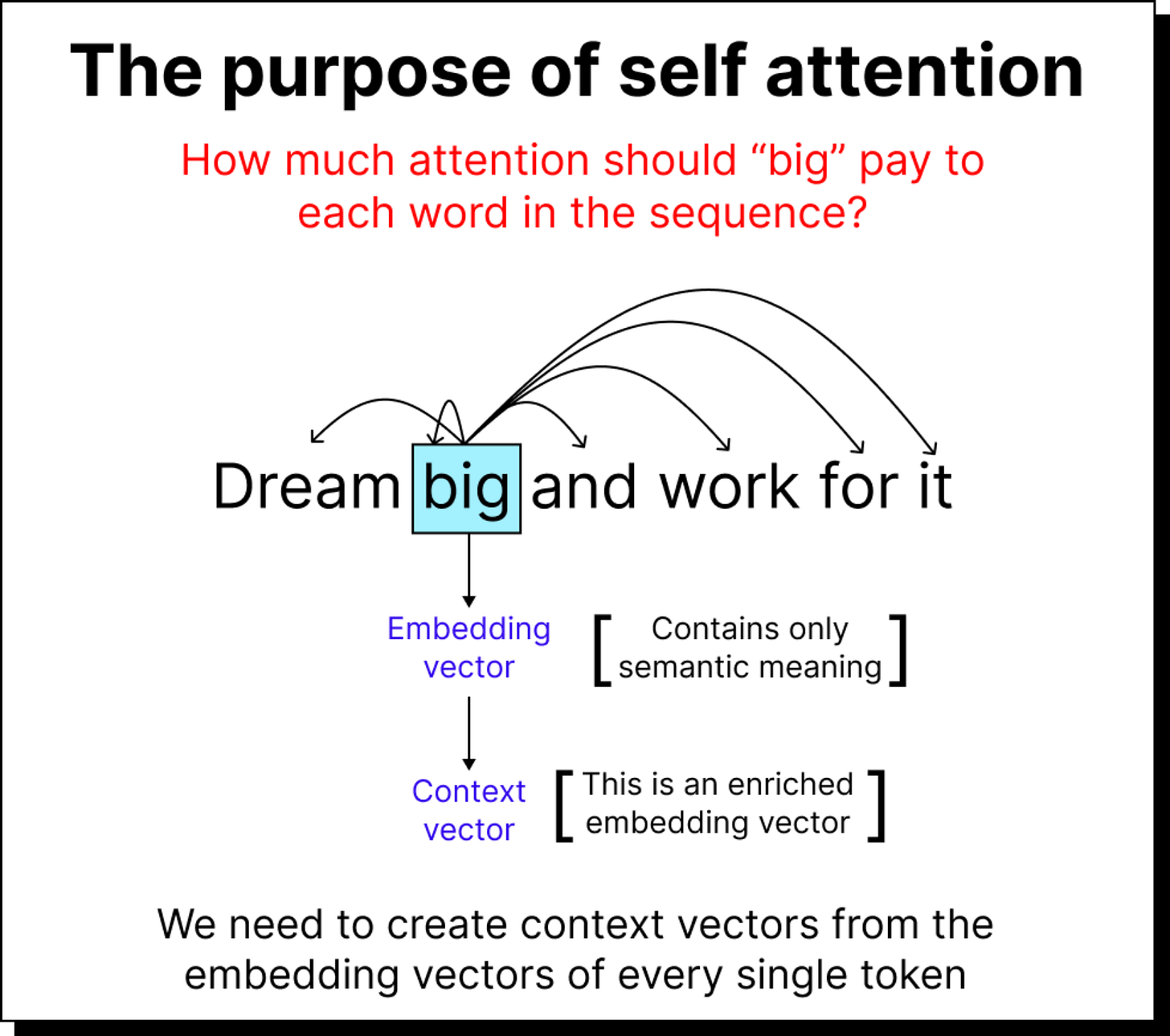
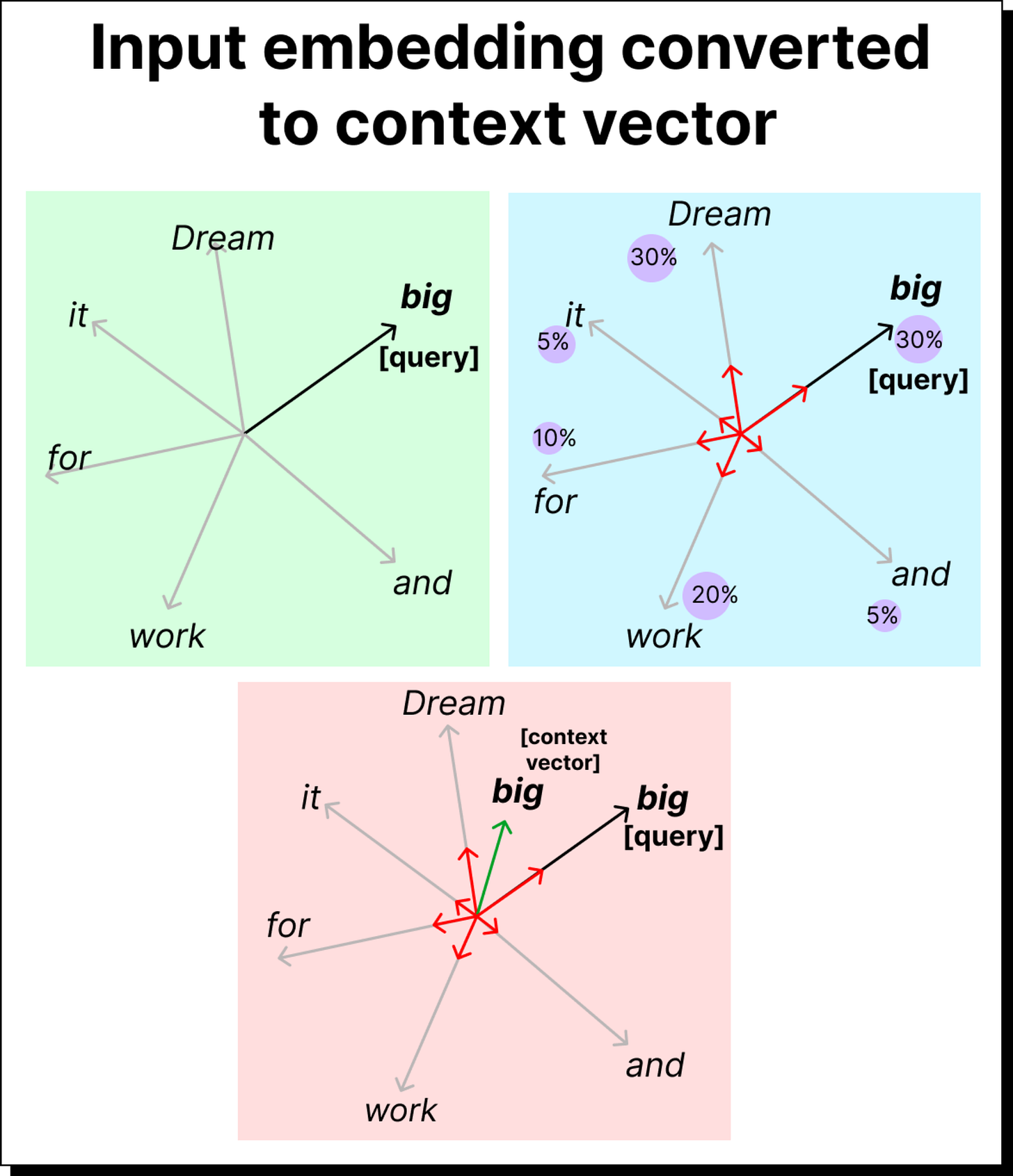
However, a word embedding alone does not include context. The word big can mean different things in “big dream” versus “big mistake.” Therefore, what we truly need are context vectors that adapt the meaning of each word based on its surroundings. This is precisely what self-attention helps us build.
The Logic of Paying Attention: Scores and Weights
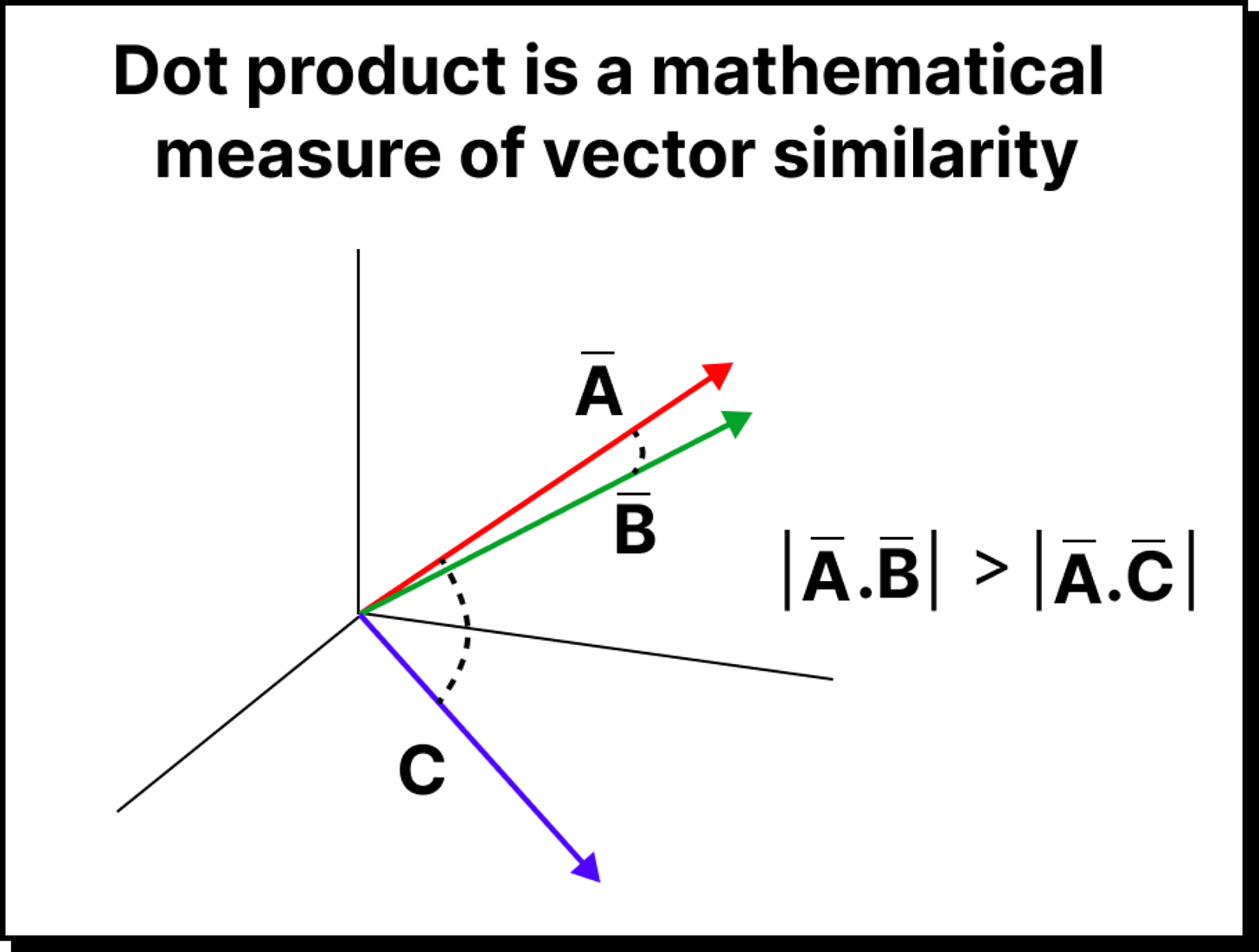
For every word acting as a query (say the word big), the model computes how much attention it should pay to every other word (called keys). To measure this, we calculate a dot product between the query vector and each key vector. The dot product serves as a mathematical proxy for similarity. If two vectors point in the same direction in the embedding space, their dot product is large, indicating a stronger relationship.
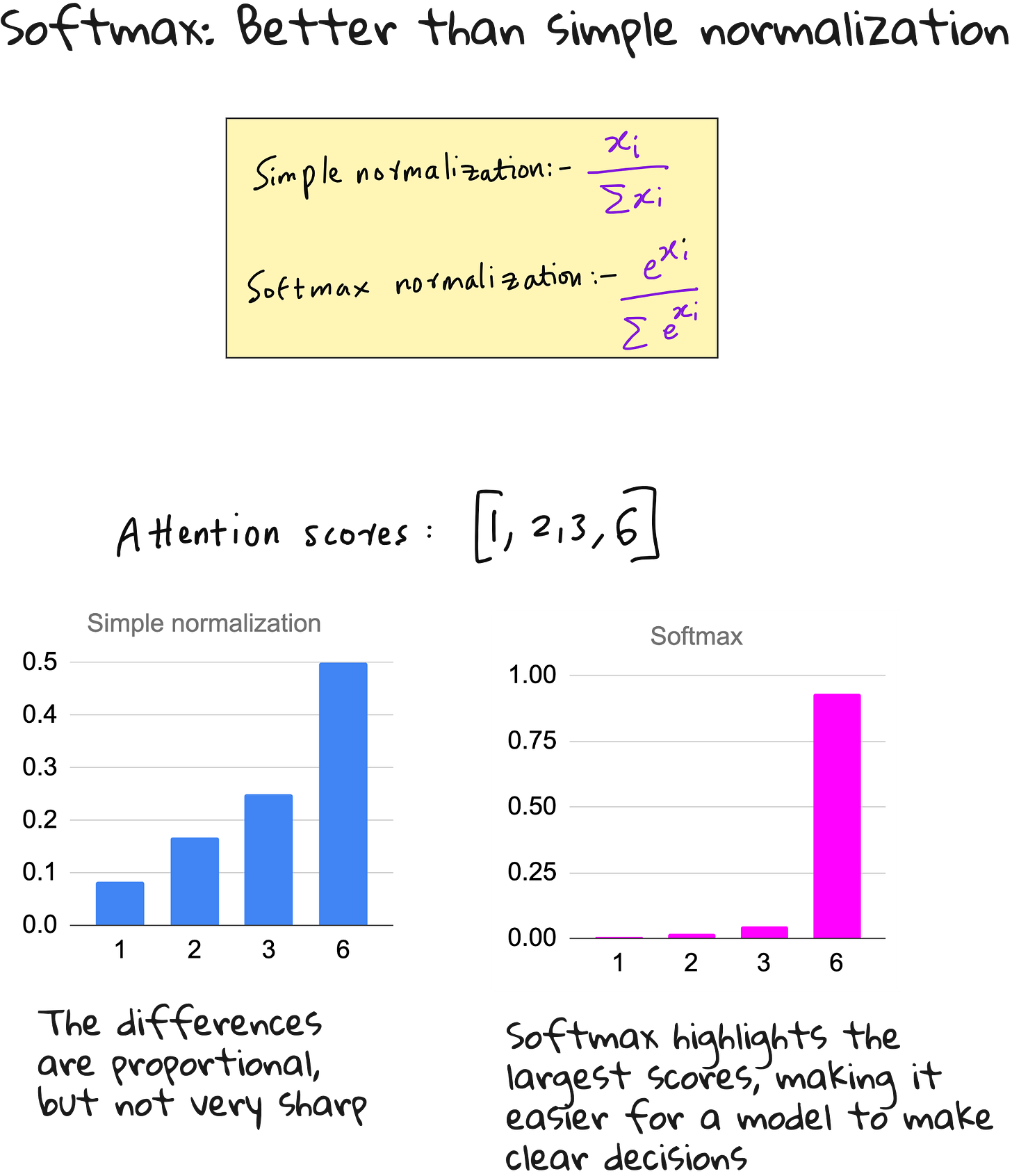
These raw dot-product values are called attention scores. But they are not immediately useful because their sum is not equal to one. To make them interpretable, we convert these scores into attention weights using normalization techniques.
The simplest way is to divide each score by the total sum, but in modern deep learning, we use a more effective method called softmax normalization. Softmax not only normalizes but also emphasizes the strongest relationships by making the highest values stand out more clearly. This gives the model the ability to focus sharply.
Building the Context Vector
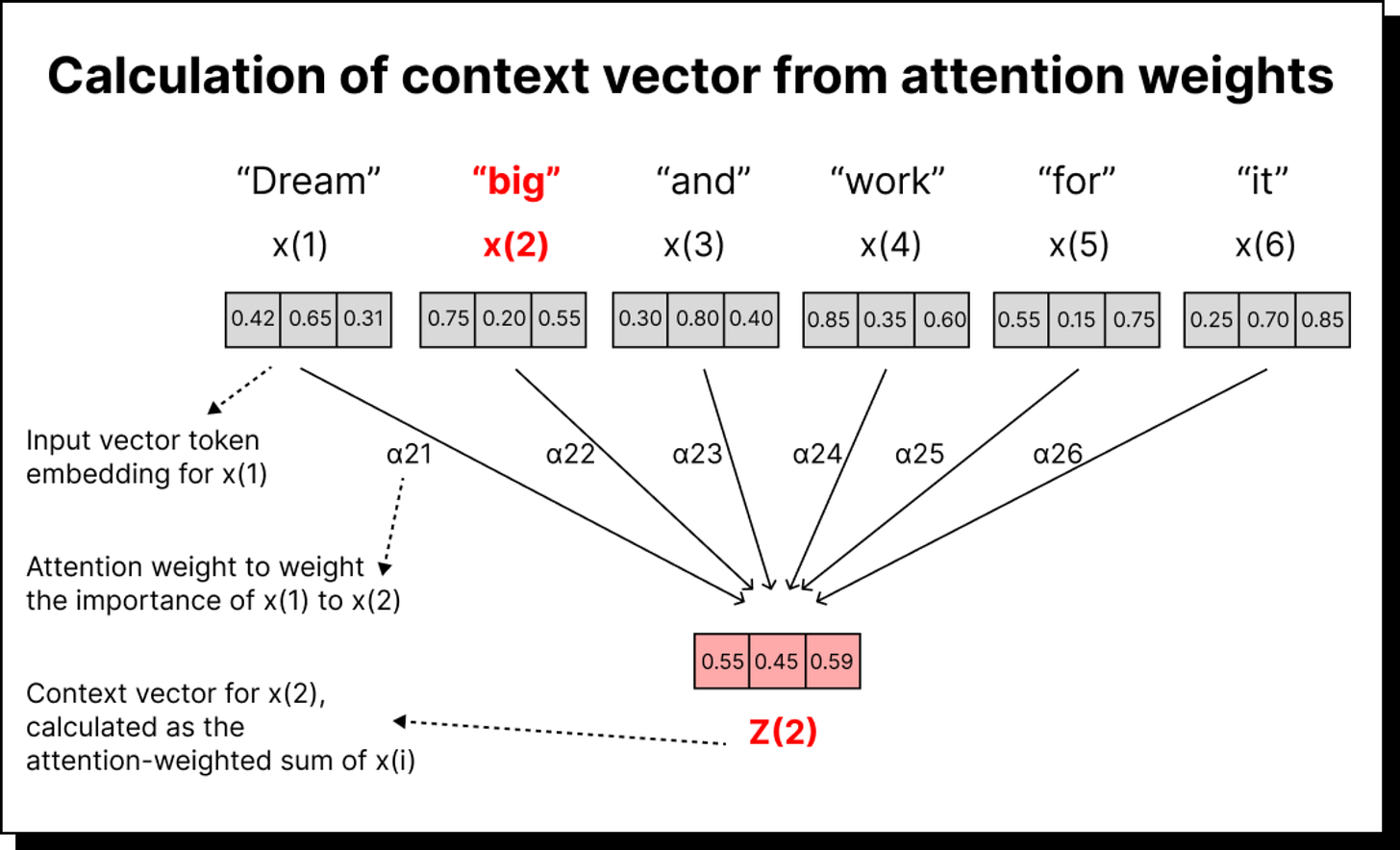
Once we have attention weights, the next step is to use them to create a context vector for each word. This is done by taking a weighted sum of all input embeddings, where the weights are the attention values. If the attention weight between big and dream is 0.3, then 30% of the dream vector contributes to the final context vector for big.
Visually, you can imagine shrinking each word’s vector based on how much attention it receives and then adding them all up. The resulting vector represents the meaning of big in the context of the sentence - enriched, contextual, and aware of its neighbors.
We repeat this process for every word in the sequence, resulting in as many context vectors as there are words. Unlike RNNs, which produce a single summary vector for the entire sentence, self-attention creates one contextualized representation for each word, making it far more expressive.
The Mathematics Behind the Transformation
If we think in terms of matrices, suppose our input embedding matrix has six words, each represented by a 3-dimensional vector. That gives a shape of 6×3. The attention weights form a 6×6 matrix since each of the six words pays attention to all six words, including itself. By multiplying the 6×6 attention matrix with the 6×3 embedding matrix, we obtain a new 6×3 matrix containing the context vectors.
This simple yet elegant matrix multiplication captures the essence of self-attention: every word in the input now becomes aware of every other word through the mechanism of weighted averaging. It is both mathematically neat and conceptually powerful.
Why Self-Attention Changed Everything
The brilliance of self-attention lies in how it replaced recurrence entirely. Instead of processing words sequentially as RNNs did, attention mechanisms allow all words to interact with each other in parallel. This parallelism made training much faster and enabled models to capture long-range dependencies that RNNs could never handle efficiently.
When this concept was extended further into multi-head attention and masked self-attention, it led to the creation of the Transformer architecture, which now forms the foundation of all large language models like GPT, BERT, and others.
Closing Thoughts
Understanding self-attention is like understanding the moment when machines first learned to focus. From compressing entire sentences into one vector, we moved to letting every word attend to every other word. This evolution changed how we represent meaning, paving the way for the language models that define our present era.
The elegance of the attention mechanism lies in its simplicity — it is nothing more than dot products, softmax, and matrix multiplication — yet it captures one of the deepest ideas in human cognition: the ability to focus selectively on what truly matters.