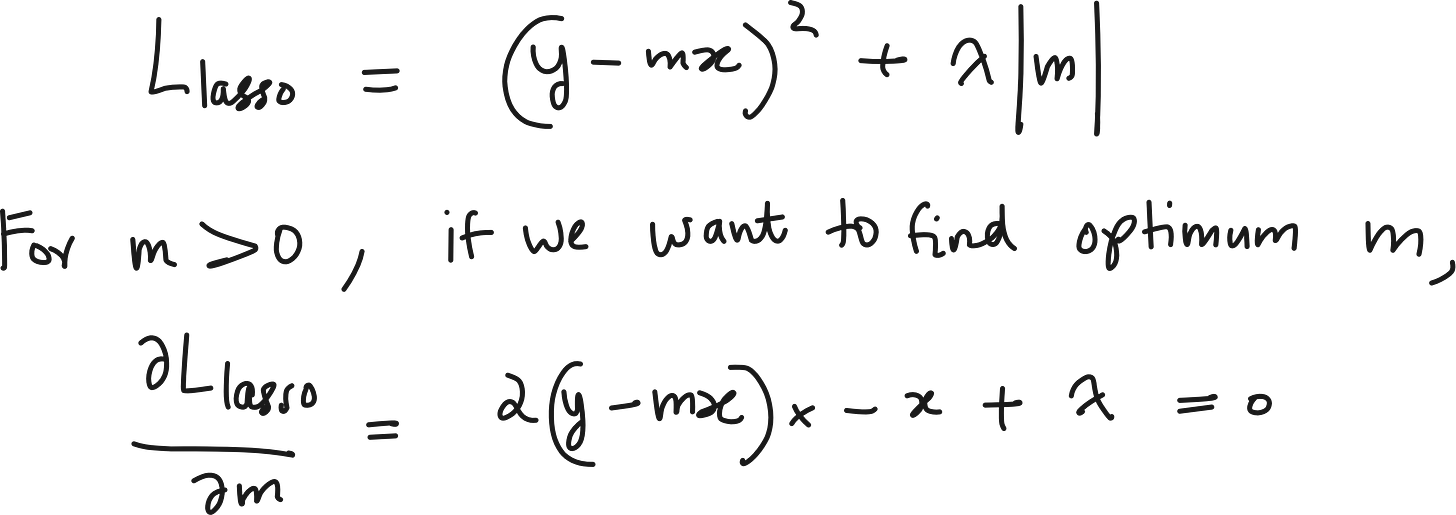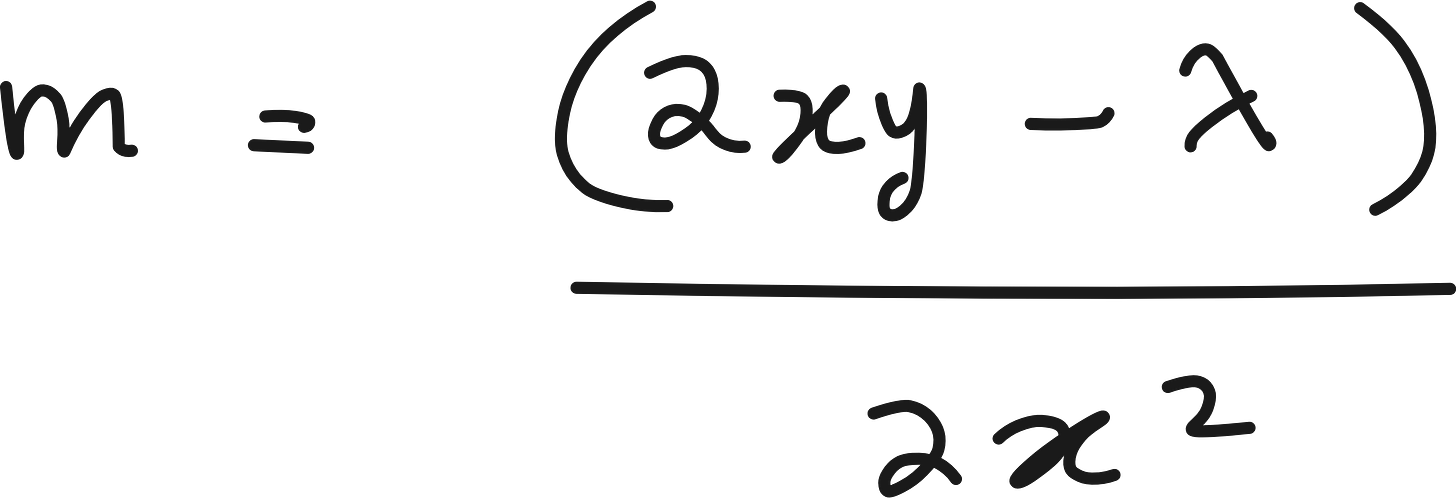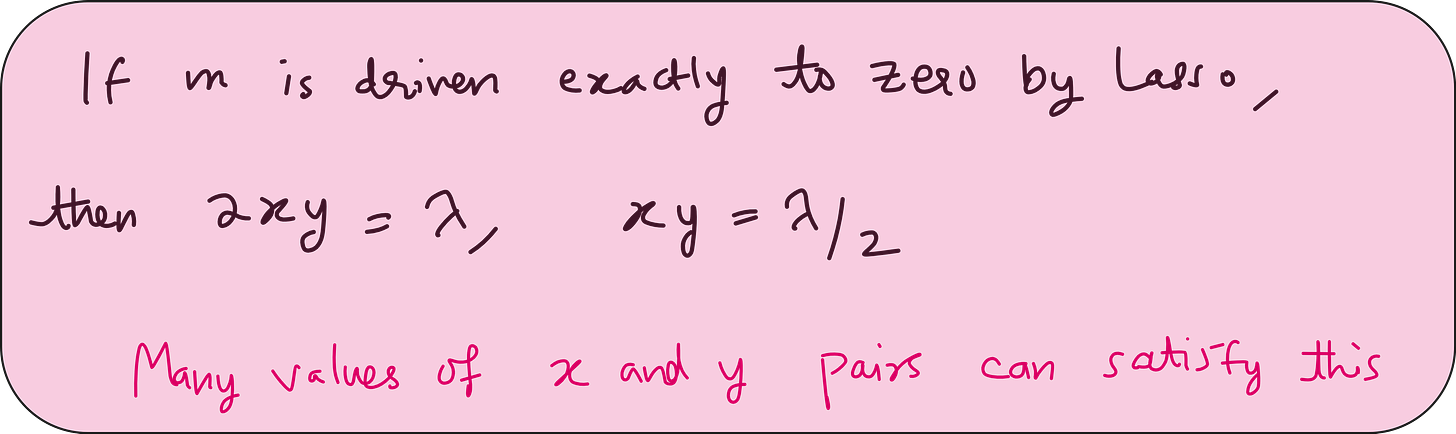If regularization is easy can you tell me why Lasso forces some parameters to exactly zero?

Regularization, Lasso regression (L1), Ridge regression (L2)

I heard “regularization” for the first time during MIT’s graduate level machine learning course in the fall of 2019.

Then I again heard that from a couple of friends who had an ML job interview. Apparently both of them were asked what is “Lasso and Ridge regression”.

It felt like regularization is an important concept that I didn’t know well.

The first thing I usually do for new topics is Google "Topic XYZ visually explained”. So I typed “Regularization visualized” and opened Google Images to see this beautiful yet horrifying figure. I had no idea what was going on!

But the math formula of regularization implementation appeared straightforward. You simply apply a penalty term to the loss function.

But here was the problem. As I learned more about Lasso, it was confusing to know that Lasso forces some model parameters to be exactly zero, whereas Ridge does not.

So I left this confusing part in the back burner to be looked at later.

Little did I know that this was the door to understanding the entire concept of regularization comprehensively. Now when I look at the above figure, I really appreciate its beauty. But for 2 or 3 years I paid no attention to it.

In this article, I will try to explain regularization in the simplest way possible. I will also cover what exactly is Lasso (L1) and Ridge (L2) regression and explain why Lasso forces some unimportant features to be exactly zero, whereas Ridge does not.

What is regularization?

Regularization is used in ML to prevent overfitting. It improves a model's ability to generalize to new, unseen data.

Regularization adds a penalty to the loss function, discouraging the model from learning overly complex patterns (or noise) that only fit the training data.

It simplifies the model by constraining its parameters, encouraging it to focus on the most important patterns in the data.

How Regularization Works?

Think about what an ML model is doing. ML models aim to minimize the loss function. Regularization modifies the loss function by adding a penalty term.

The penalty term ensures that model parameters cannot become very high to fit noisy data because that will increase the loss. Here λ is the Regularization strength that controls the trade-off between the original loss and the penalty.

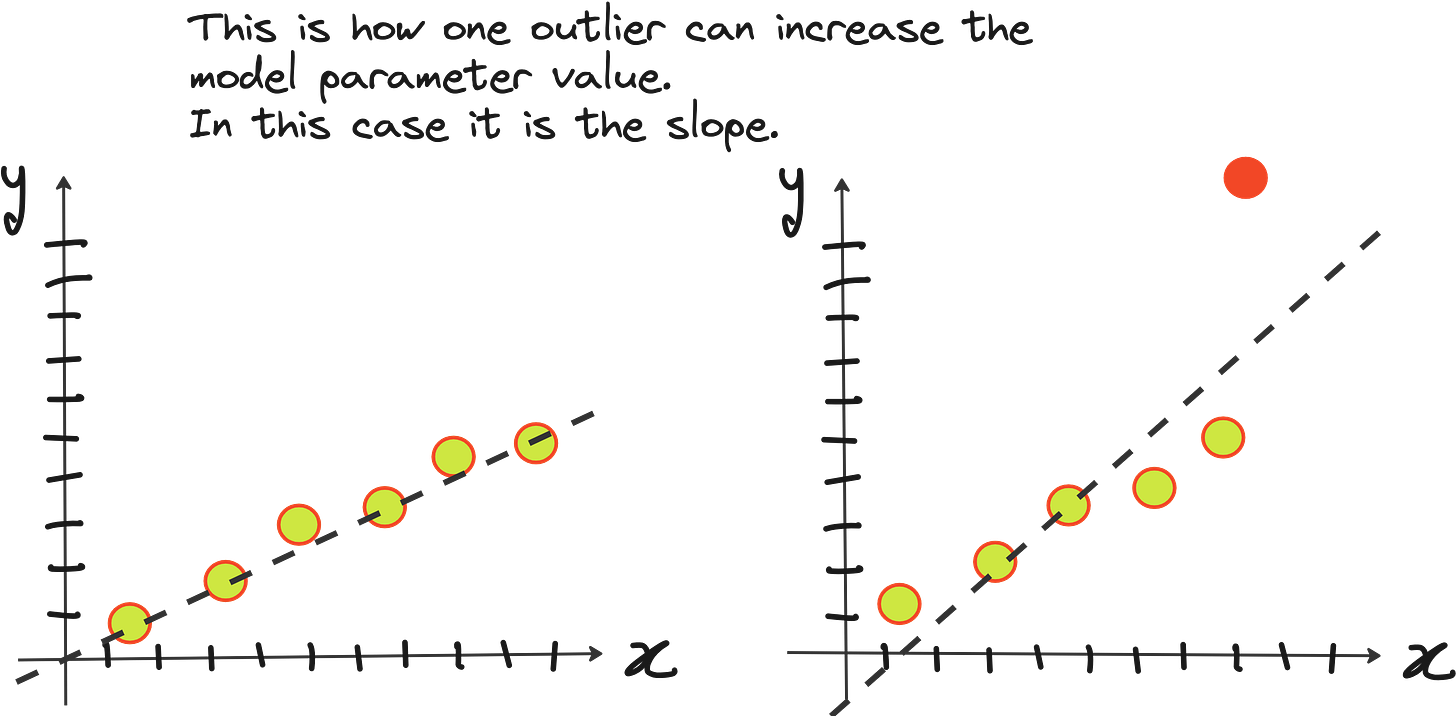
But here is a question. How does fitting noisy data makes model parameters high? Here is a simple example.

Types of regularization

Ridge regression (L2 regularization)

Ridge Regularization (L2 Regularization) modifies the linear regression loss function by adding an L2 penalty (sum of squared weights).

If λ = 0 ridge is reduced to a normal linear regression.

If λ is large, the model shrinks all weights close to 0 to prevent overfitting.

Lasso regression (L1 regularization)

Lasso Regularization (L1 Regularization) uses an L1 penalty, which adds the absolute values of the weights.

Small λ means less penalty. Behaves like linear regression.

If λ is large, the model shrinks some weights to be exactly zero. Effectively performing feature selection. Because if weights are zero, those features are not used for making predictions.

But here is the million dollar question. How the heck does Lasso shrinks some weights to exactly 0 whereas Ridge only makes it approximately zero? This question frustrated me for quite some time.

If you can wrap your head around the answer to this, you are awesome.

Why exactly does Lasso set some weights to zero but not Ridge?

Here is a mathematical way to look at it

Consider Ridge first.

Assume an overly simple linear fit to a data point.

To find the optimum ‘m’ that minimize the loss, we need to take the derivative of loss with respect to ‘m’.

Thus Ridge regression can make the model parameter small for big values of λ, but it does not push the parameters to be exactly zero.

Now consider Lasso.

There are many values of x and y pairs where it is possible to have m = 0 even when λ is big. This is the mathematical intuition behind Lasso forcing some weights or parameters to be exactly zero.

Mathematical intuition is good, but it is still not the best kind of intuition right?

So here is a graphical intuition

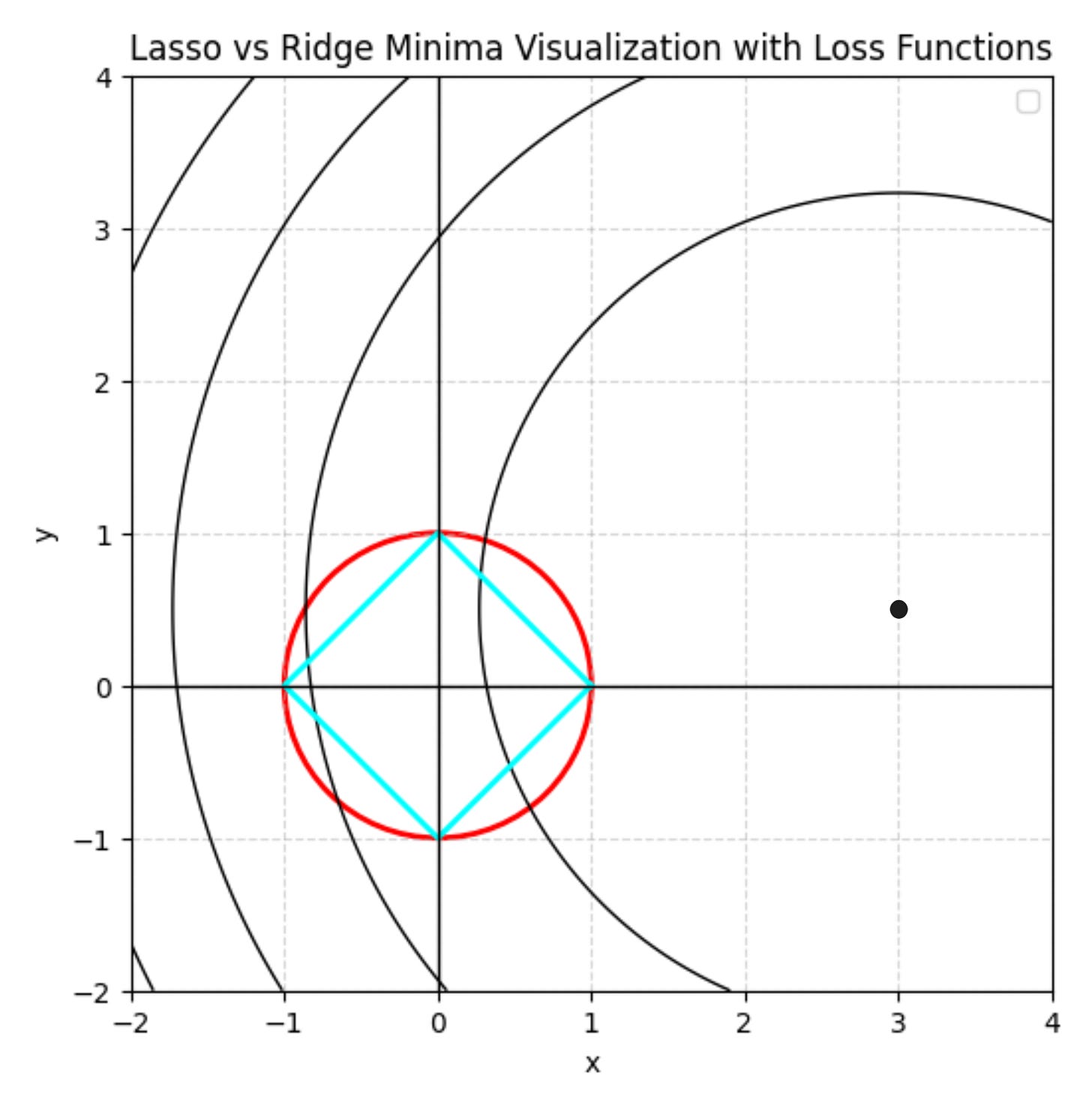
Consider a custom loss function.

The minimum of this loss function occurs at (x, y) = (3, 0.5)

We can plot the iso-contours of this function. They will look like this.

Now consider Lasso and Ridge formulae for this case.

The penalty terms for both Ridge and Lasso become minimum when (x, y) = (0, 0). When λ→∞ the entire Loss term is very close to penalty term. Thus the minimum of the whole loss function is close to (x = 0, y = 0)

The nominal loss (non-regularized loss) term becomes minimum when (x, y) = (3, 0.5). This happens when λ=0.

So for intermediate values of λ, the minimum is somewhere between (0, 0) and (3, 0.5).

Now let us make 3 assumptions for making the intuition simpler.

1. Say λ = 1,

2. The value of the Ridge penalty term = 4 and

3. The value of the Lasso penalty term = 2

• For Ridge, this means you are looking at a circle centered at the origin with radius = 2.

• For Lasso, you are looking at a diamond-like shape whose 4 corners are at (2, 0), (0, -2), (-2, 0) and (0, 2).

For all points along the red circle you have the same penalty for Ridge regression.

However you don’t want to stray away from the minima (x=3, y=0.5) of the non-regularized loss function because the farther you are from that point, the the higher the contribution to the loss by the un-regularized term.

Now look at the red circle and blue diamond.

If you are on the circle, you do not minimize the total loss by making the ‘y’ component exactly zero. You minimize the total loss if you have a small non-zero value for the ‘y’ component. Please remember that here ‘x’ and ‘y’ are not input-output pairs, they are 2 of the model parameters used in the loss function.

You can see that the red dot whose ‘y’ coordinate is non-zero is closer to the black dot at (x = 3, y = 0.5) that the blue dot whose ‘y’ coordinate. Just look at the radius of the dotted iso-contour circles.

Similarly, if you are on the blue diamond, you minimize the total loss by staying on the diamond and making the ‘y’ component exactly zero. You are closest to the minima (x = 3, y = 0.5) when you drive the value of ‘y’ to be exactly zero.

This example demonstrates how Lasso is incentivized to drive some weak features to be exactly zero and how Ridge is incentivized to keep then small, but non-zero.

Fascinating right?

I highly recommend you to check out this article from explained.ai. It is simply brilliant. They have brilliant visuals that I haven’t showed you.

How do you select a good value for λ?

There is no strict rule. But here are the primary considerations.

Here are some practical recommendations

For Ridge and Lasso consider this practical insights if you were to implement then using scikit learn in Python.

I have published a simple and detailed video on regularization on Vizuara’s YouTube channel. Highly recommend you to check it out. I am sure you will enjoy.