𝗨𝗻𝗱𝗲𝗿𝘀𝘁𝗮𝗻𝗱𝗶𝗻𝗴 𝘁𝗵𝗲 𝗕𝗶𝗮𝘀-𝗩𝗮𝗿𝗶𝗮𝗻𝗰𝗲 𝗧𝗿𝗮𝗱𝗲𝗼𝗳𝗳 𝗶𝗻 𝗣𝗼𝗹𝘆𝗻𝗼𝗺𝗶𝗮𝗹 𝗥𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻
When implementing linear regression, we often encounter scenarios where the model fails to achieve the desired R² score. This is usually because the data does not adhere to the linearity assumption. To address this, polynomial regression can be employed.
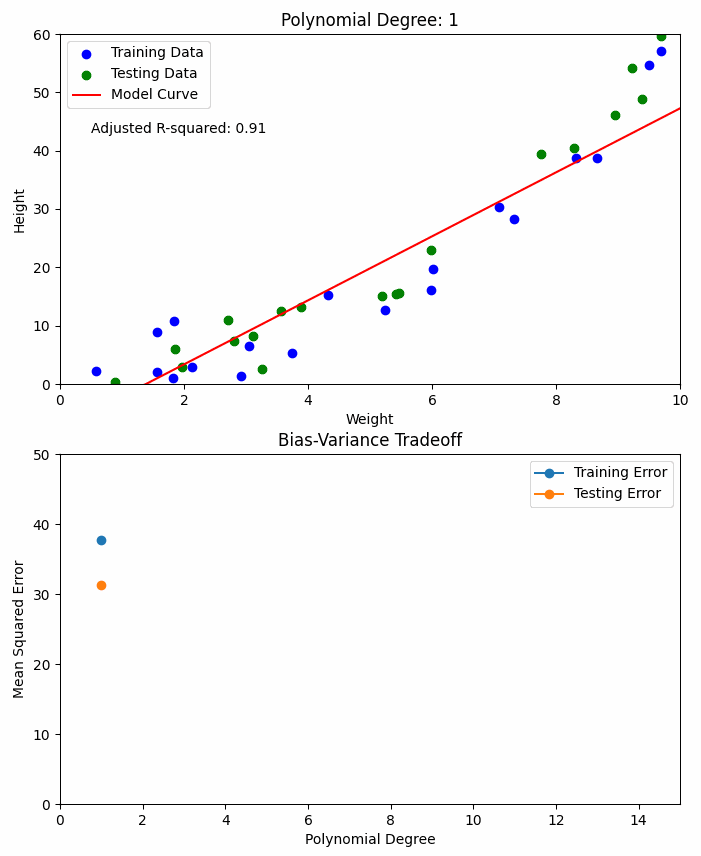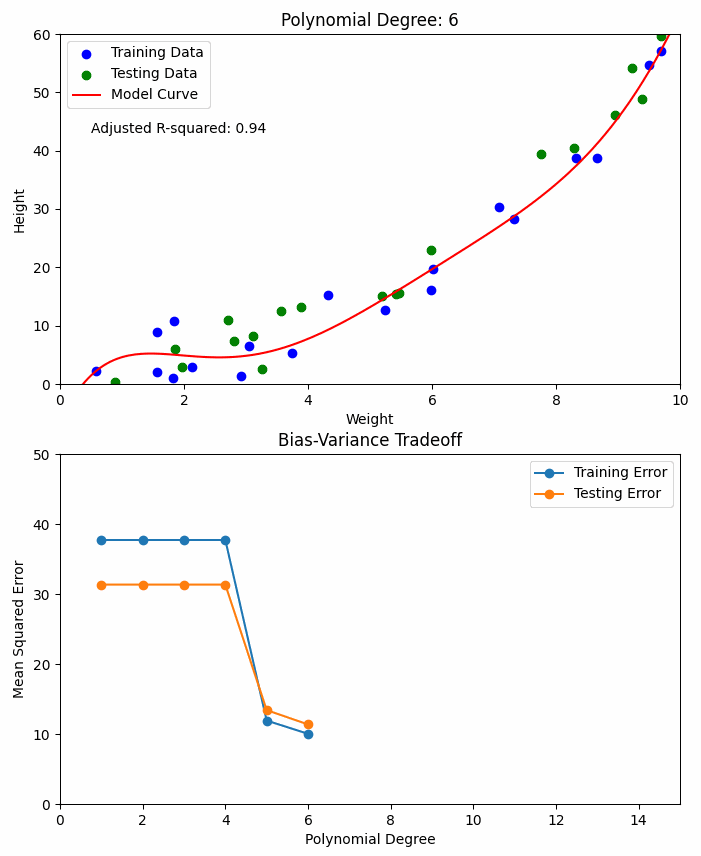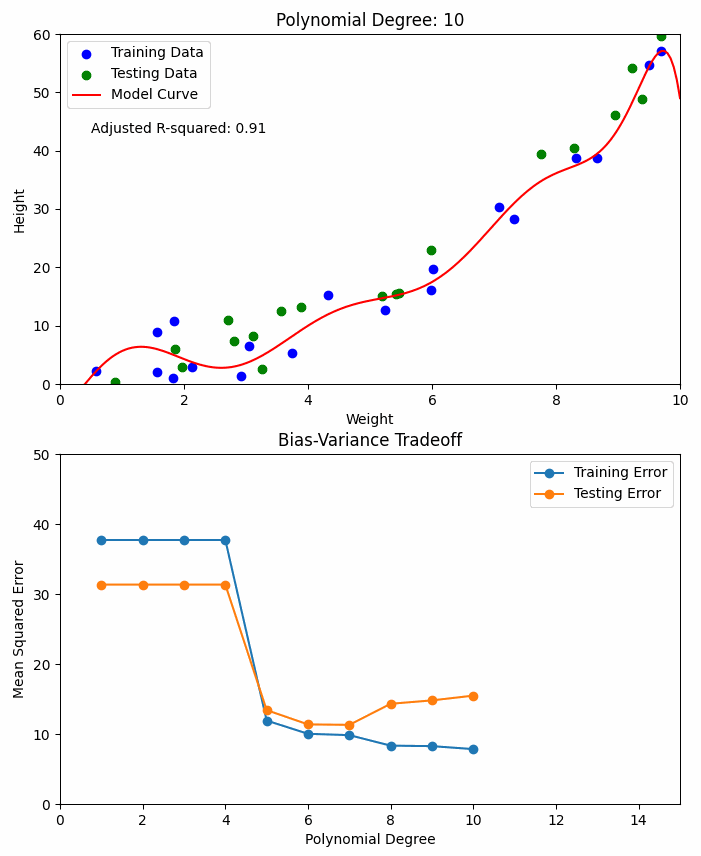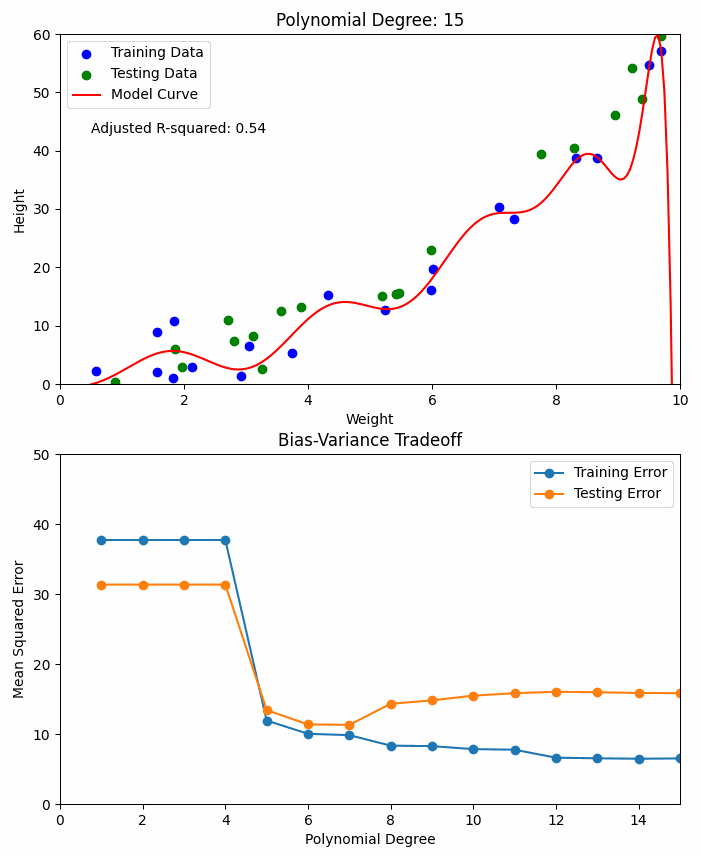
By introducing polynomial features into the dataset, the model is capable of fitting a curve instead of a straight line. The degree of the polynomial determines how much curvature the model can capture.
𝗛𝗶𝗴𝗵-𝗱𝗲𝗴𝗿𝗲𝗲 𝗽𝗼𝗹𝘆𝗻𝗼𝗺𝗶𝗮𝗹𝘀 provide high accuracy (low bias) but may lead to overfitting (high variance).
𝗟𝗼𝘄-𝗱𝗲𝗴𝗿𝗲𝗲 𝗽𝗼𝗹𝘆𝗻𝗼𝗺𝗶𝗮𝗹𝘀 ensure low variance but might result in underfitting (high bias).
Striking the right balance between bias and variance is crucial—this is referred to as the Bias-Variance Tradeoff.
For a comprehensive understanding of this concept, check out this tutorial:
📽️ 𝗣𝗼𝗹𝘆𝗻𝗼𝗺𝗶𝗮𝗹 𝗥𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻: Complete Tutorial | Adjusted R² | 𝗕𝗶𝗮𝘀-𝗩𝗮𝗿𝗶𝗮𝗻𝗰𝗲 𝗧𝗿𝗮𝗱𝗲𝗼𝗳𝗳 by Pritam Kudale:
I've also made the code for the animation in the video available for you to experiment with. You can find it here:
💻 𝗣𝗼𝗹𝘆𝗻𝗼𝗺𝗶𝗮𝗹 𝗥𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻 𝗔𝗻𝗶𝗺𝗮𝘁𝗶𝗼𝗻 𝗖𝗼𝗱𝗲: click here